92) Ache a área da região limitada pelo laço da curvas .
Passo 1
A função que irá nos fornecer a área será:
Integrando por substituição e substituindo os limites:
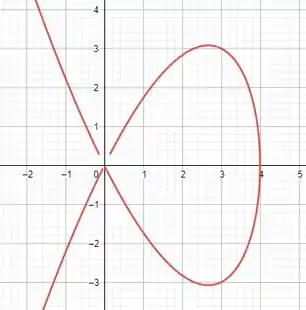
Veja o esboço das curvas para uma melhor compreensão:
92) Ache a área da região limitada pelo laço da curvas .
A função que irá nos fornecer a área será:
Integrando por substituição e substituindo os limites:
Veja o esboço das curvas para uma melhor compreensão:
