Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.1 - Ex. 54

Encontre a área da região delimitada pelas curvas dadas.

y = 4 ln ⁡ x ,   y = x ² ln ⁡ x

Passo 1

Fala aí! tudo certinho?

Nesse problema temos que calcular a area entre as curvas y = 4 ln ⁡ x e y = x 2 ln ⁡ x .

Tem ideia de como fazemos isso?

Para calcular a área entre as curvas fazemos

A = ∫ a b y 1 - y 2 d x

Com essas limitações conseguimos esboçar a seguinte figura:

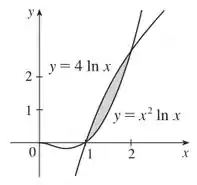
Portando y 1 = 4 ln ⁡ x e y 2 = x 2 ln ⁡ x

Veja só!

Passo 2

Primeiro a gente encontra os pontos onde as curvas se interceptam, aí a gente acha o intervalo em que ela está limitada! Elas se encontram nos pontos que se igualam, então

x 2 ln ⁡ x = 4 ln ⁡ x  

x 2 ln ⁡ x - 4 ln ⁡ x = 0

x 2 - 4 ln ⁡ x = 0

Assim, desde que x seja maior que zero, temos que x = 1 ou x = 2 , então esses são os limites da nossa função! Para 1 < x < 2 ,   4 ln ⁡ x > x 2 ln ⁡ x . A gente consegue ver isso pela figura, pois a curva de 4 ln ⁡ x está à esquerda da x 2 ln ⁡ x .

Sendo assim, nossa área é

A = ∫ 1 2 ( 4 ln ⁡ x - x 2 ln ⁡ x ) d x = ∫ 1 2 [ 4 - x 2 ln ⁡ x ] d x

Para resolver a gente utiliza as famosas substituições:

u = ln ⁡ x ,   d v = 4 - x 2 d x → d u = 1 2 d x ,   v = 4 x - 1 3 x 3

Bora lá!

Passo 3

Substituindo, nossa área será:

A = ln ⁡ x 4 x - 1 3 x 3 1 2 - ∫ 1 2 4 x - 1 3 x 3 1 x d x

A = ln ⁡ 2 16 3 - 0 - ∫ 1 2 4 - 1 3 x 2 d x

A = 16 2 ln ⁡ 2 - 4 x - 1 9 x 3 1 2

Simplificando...

A = 16 3 ln ⁡ 2 - 64 9 - 35 9

A = 16 3 ln ⁡ 2 - 29 9

E aí! entendeu tudo? Responde Aí!

Resposta

A = 16 3 ln ⁡ 2 - 29 9 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o cálculo para encontrar a área do triângulo com os vértices dados. 0,0 ,3,1 ,( 1,2 )
Use um gráfico para estimar a intersecção com o eixo x da curva y = 1 - 2 x - 5 x 4 . A seguir, use essa informação para estimar a área da região que se situa sob a curva e acima do eixo x.
Esboce a região delimitada pelas curvas indicadas. Decida quando integrar em relação a x ou y. Desenhe um retângulo aproximante típico e identifique sua altura e largura. Então, calcule a área da regi
Esboce a região delimitada pelas curvas indicadas. Decida quando integrar em relação a x ou y. Desenhe um retângulo aproximante típico e identifique sua altura e largura. Então, calcule a área da regi
Esboce a região delimitada pelas curvas indicadas. Decida quando integrar em relação a x ou y. Desenhe um retângulo aproximante típico e identifique sua altura e largura. Então, calcule a área da regi