Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.1 - Ex. 53

Encontre a área da região delimitada pelas curvas dadas.

y = e - 0.4 x ,   y = 0 ,   x = 5

Passo 1

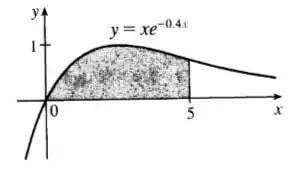
Com essas limitações conseguimos esboçar a seguinte figura:

Passo 2

Como a nossa função varia em x entre 0 e 5 , teremos a seguinte área:

A = ∫ 0 5 x e - 0.4 x d x

Para resolver a gente utiliza as famosas substituições:

u = x ,   d v = e - 0.4 x d x → d u = d x ,   v = - 2.5 e - 0.4 x

Passo 3

Portanto, nossa área será:

- 2.5 x e - 0.4 x 0 5 + 2.5 ∫ 0 5 e - 0.4 x d x = 12.5 e - 2 + 0 + 2.5 - 2.5 e - 0.4 x 0 5 =

- 12.5 e - 2 - 6.25 e - 2 - 1 = 6.25 - 18.75 e - 2

ou

25 4 - 75 4 e - 2

Resposta

A = 6.25 - 18.75 e - 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região delimitada pelas curvas indicadas. Decida quando integrar em relação a x ou y. Desenhe um retângulo aproximante típico e identifique sua altura e largura. Então, calcule a área da regi
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = x , y = 1 2 x , x = 9
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = x , y = x 2 - 2
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = cos ⁡ x , y = 1 - cos ⁡ x , 0 ≤ x ≤ π
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = 1 x , y = x , y = 1 4 x ,x0