Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.3 - Ex. 37

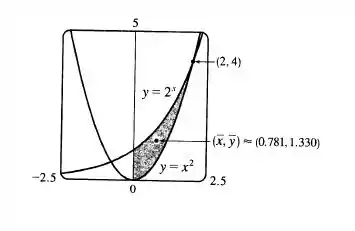
Calcule o centroide da região limitada pelas curvas y = 2 x e y = x 2 , 0 ≤ x ≤ 2 , com precisão de três casas decimais. Esboce a região e marque o centroide para ver se sua resposta é razoável.

Passo 1

Bom galera, nessa questão iremos calcular as coordenadas do centroide da função apresentada. Após encontrar as coordenadas, iremos esboçar graficamente a função para conferir a resposta.

Passo 2

Por definição de área entre curvas, podemos calcular a área da região da seguinte maneira

A = ∫ 0 2 2 x - x 2 d x

Dessa forma, temos

A = 2 x ln ⁡ 2 - x 3 3 0 2 = 3 ln ⁡ 2 - 8 3 = 1.661

Podemos encontrar x - da seguinte maneira

x - = 1 A ∫ 0 2 x 2 x - x 2 d x

Resolvendo a integral, temos

x - = 1 A x 2 x ln ⁡ 2 - 2 x ln ⁡ 2 2 - x 4 4 0 2 = 0.781

Passo 3

Podemos encontrar y - da seguinte maneira

y - = 1 A ∫ 0 2 2 x - x 2 2 d x

Resolvendo a integral, temos

y - = 1 2 A 2 2 x 2 ln ⁡ 2 - x 5 5 0 2 = 1.330

Esboçando graficamente, temos

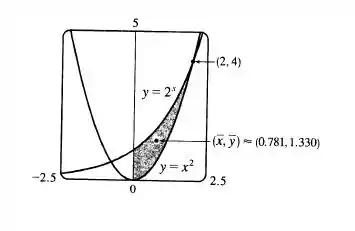
Resposta

x - ,   y - = 0.781 ,   1.330

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região delimitada pelas curvas indicadas e encontre sua área. x = y 4 , y = 2 - x , y = 0
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = cos ⁡ π x , y = 4 x 2 - 1
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área correta até a quinta casa decimal. y = e 1 - x 2 ,y = x 4
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área correta até a quinta casa decimal. y = tan 2 ⁡ x ,y = x
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = cos ⁡ x , y = sin ⁡ 2 x , x = 0 ,x = π 2