Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 49

Ache a área da região limitada pelas parábolas y 2 = 4 p x e x 2 = 4 p y .

Passo 1

Vamos olhar o gráfico das duas funções sobreposto um ao outro (sem perda de generalidade, para simplificar, vamos analisar o caso de p = 1 ):

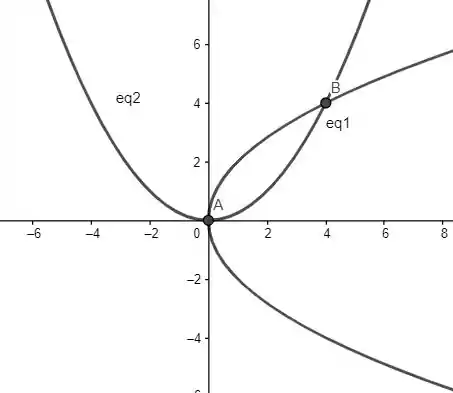
Passo 2

Seja A a origem e B o ponto de interseção entre as parábolas:

Vamos encontrar o ponto A :

A = ( 0,0 )

Vamos encontrar o ponto B:

y 2 = 4 p x x 2 = 4 p y

B = ( 4 p , 4 p )

Passo 3

Para calcular a área S em questão, basta resolver a integral:

S = ∫ 0 4 p ( x 2 4 p - 4 p x ) d x

S = ∫ 0 4 p ( x 2 4 p ) d x - ∫ 0 4 p ( 4 p x ) d x

S = x 3 12 p 0 4 p - 2 3 4 p 1 2 x 3 2 0 4 p

S = 16 p 2

Resposta

A área S , em unidades de área do gráfico, é:

S = 16 p 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = tg ⁡ xex = 0ey = 1
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x = y 2ey = - x 2
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = cosh ⁡ xey = senh ⁡ x ,x = - 1ex = 1
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = cos ⁡ x ,y = - 3 5 π x + 3 10 ,x ∈ π 2 , 4 π 3
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x = y 2 + 1ex + y = 7