Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 43

Ache a área da região limitada pelas três curvas y = x 2 ,   y = 8 - x 2   e   4 x - y + 12 = 0 .

Passo 1

Observando o gráfico de cada curva, teremos:

Curva 1 - y = x 2 → f 1 x = x 2 :

Curva 2 - y = 8 - x 2 → f 2 x = 8 - x 2 :

Curva 3 - 4 x - y + 12 = 0 → f 3 x = 4 x + 12 :

Passo 2

Calculando os pontos de interseção:

Curva 1 e Curva 2:

x 2 = 8 - x 2 → 2 x 2 = 8 → x 2 = 4 → x = ± 2 → A = 2,4   e   B = ( - 2,4 )

Curva 1 e Curva 3:

4 x + 12 = x 2 → x 2 - 4 x - 12 = 0 → x = - b ± b 2 - 4 a c 2 a → x = - ( - 4 ) ± - 4 2 - 4.1 . - 1 2 2.1

→ x = 6   o u   x = - 2 → B = - 2,4   e   C = ( 6,36 )

Curva 2 e Curva 3:

4 x + 12 = 8 - x 2 → x 2 + 4 x + 4 = 0 → x + 2 2 = 0 → x = - 2 → B = ( - 2,4 )

Passo 3

Juntando os três gráficos, teremos:

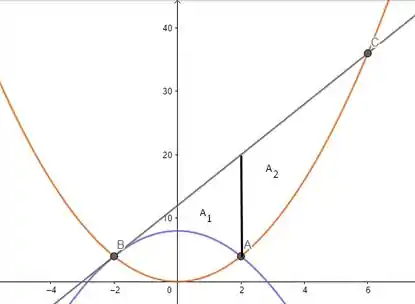
Dessa maneira, teremos que dividir em dois intervalos:

  1. - 2 ≤ x < 2

    2. Nesse intervalo, a área desejada estará entre as curvas 3 e 2, daí teremos:

    A = ∫ f x d x   e   f x = f 3 x - f 2 ( x )

    A = ∫ - 2 2 4 x + 12 - 8 - x 2 d x → ∫ - 2 2 x 2 + 4 x + 4 d x = x 3 3 + 2 x 2 + 4 x 2 - 2 →

    A = 2 3 3 + 2 . 2 2 + 4.2 - - 2 3 3 + 2 - 2 2 + 4 - 2 = 56 3 - - 8 3 → A 1 = 64 3 u . a .

  2. 2 ≤ x ≤ 6

Nesse intervalo, a área desejada estará entre as curvas 3 e 1, daí teremos:

A = ∫ f x d x   e   f x = f 3 x - f 1 ( x )

A = ∫ - 2 2 4 x + 12 - x 2 d x → A = ∫ - 2 2 ( - x 2 + 4 x + 12 ) d x = - x 3 3 + 2 x 2 + 12 x 6 2 →

A = - 6 3 3 + 2 . 6 2 + 12.6 - - 2 3 3 + 2 . 2 2 + 12.2 = 216 3 - 88 3 → A 2 = 128 3

Logo, a área total será A = A 1 + A 2 = 192 3   u . a .

Resposta

A área total será A = 192 3   u . a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área sob a curva f x = y acima do intervalo dado. f x = x, [ 1 ,9 ]
Encontre a área sob o gráfico de f x = 4 x - x 2 , acima do intervalo [ 0 ,4 ] usando a Definição 5.4 . 3 , tomando x k * como sendo a extremidade direita de cada subintervalo.
Use um recurso computacional para encontrar as aproximações pelas extremidades esquerda, direita e pelo ponto médio da área abaixo da curva y = f ( x ) acima do intervalo dado, usando n = 10 subinterv
Use um recurso computacional para encontrar as aproximações pelas extremidades esquerda, direita e pelo ponto médio da área abaixo da curva y = f ( x ) acima do intervalo dado, usando n = 10 subinterv
Esboce a curva e encontre a área total entre ela e o intervalo dado no e i x ox . y = x 2 - 1 , [ 0 ,3 ]