Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 46
Ache a área da seção limitada pelas curvas e entre dois pontos de interseção consecutivos.
Passo 1
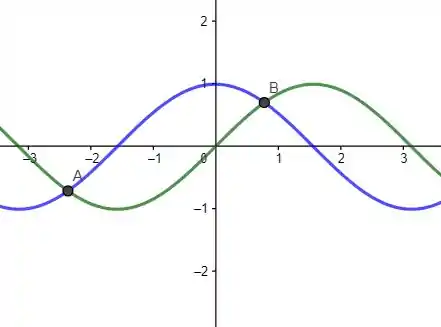
Vamos olhar o gráfico das duas funções sobreposto um ao outro:
Passo 2
Vamos encontrar os pontos A e B:
Como ,
Sem perda de generalidade, podemos calcular a área entre A e B, já que as funções são periódicas e o gráfico se repete a medida que o valor de aumenta. Nesse caso, teremos:
Passo 3
Para calcular a área em questão, basta resolver a integral:
Resposta
A área , em unidades de área do gráfico, é:
Exercícios de Livros Relacionados
7-18 Esboce a região englobada pelas curvas e encontra a área7. y = x 2 , y = x , x = 1 4 , x = 1
19-26.19. Use um recurso gráfico computacional, quando necessário, para encontra a região englobada pelas curvas.19. y = x 3 - 4 x 2 + 3 x
7-18 Esboce a região englobada pelas curvas e encontra a área11. x = sin y , x = 0 , y = π / 4 , y = 3 π / 4
19-26.Use um recurso gráfico computacional, quando necessário, para encontra a região englobada pelas curvas.22. y = x 3 - 4 x ,y = 0
7-18 Esboce a região englobada pelas curvas e encontra a área13. y = e x , y = e 2 x , x = 0 , x = ln 2 .