Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.2 - Ex. 29

  1. Se a > 0 , ache a área da superfície gerada pela rotação da curva 3 a y 2 = x a - x 2 em torno do eixo x
  2. Encontre a área da superfície se a rotação for em torno do eixo y

Passo 1

  1. Podemos ver que se a > 0 , então a curva 3 a y 2 = x a - x 2 só tem pontos para x ≥ 0 .

Vamos isolar y 2 na equação da curva, isso será útil la na frente

y 2 = x a - x 2 3 a

Vamos fazer um esboço da curva pra gente conseguir ver melhor o que que está acontecendo

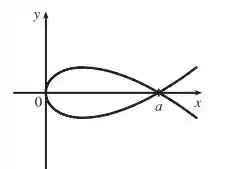
A curva é simétrica em relação ao eixo x (já que a equação é inalterada quando y é substituído por - y ). y = 0 quando x = 0 ou a , então o loop da curva estende de x = 0 a x = a .

Vamos calcular a derivada da função

d d x 3 a y 2 = d d x x a - x 2

6 a y d y d x = 2 x a - x - 1 + a - x 2

d y d x = a - x - 2 x + a - x 6 a y

Elevando ambos os lados ao quadrado, ficamos com

d y d x 2 = a - x 2 a - 3 x 2 36 a 2 y 2

Lembra que isolamos y 2 no inicio?! Agora vamos substituir 1 / y 2

d y d x 2 = a - x 2 a - 3 x 2 36 a 2 y 2 = a - x 2 a - 3 x 2 36 a 2 ⋅ 3 a x a - x 2 = a - 3 x 2 12 a x

Agora, vamos adicionar 1 unidade em ambos os lados da equação, daí ficamos com

1 + d y d x 2 = 1 + a - 3 x 2 12 a x = 12 a x 12 a x + a - 3 x 2 12 a x = a 2 + 6 x + 9 x 2 12 a x = a + 3 x 2 12 a x

Passo 2

  1. Precisamos lembrar como é a área de uma superfície de revolução, que é da seguinte forma

    2. S = ∫ c d 2 π y 1 + d y d x 2   d x

    Então, substituindo o que já calculamos, ficamos com

    S = 2 π ∫ 0 a y d s = 2 π ∫ 0 a x a - x 3 a ⋅ a + 3 x 2 12 a x d x = 2 π ∫ 0 a x a - x 3 a ⋅ a + 3 x 12 a x = 2 π ∫ 0 a a - x a + 3 x 6 a d x = π 3 a ∫ 0 a a 2 + 2 a x - 3 x 2 d x = π 3 a a 2 x + a x 2 - x 3 0 a = π 3 a a 3 + a 3 - a 3 = π 3 a a 3 = π 3 a 2

    Note que giramos a metade superior do loop em torno do eixo x . Isso gera a superfície total.

    Passo 3

  2. Precisamos girar o loop completo em torno do eixo y , de modo que obtemos o dobro da área obtida girando a metade superior do loop

S = 2 ⋅ 2 π ∫ 0 a x   a + 3 x 2 12 a x d x = 4 π ∫ 0 a x ⋅ a + 3 x 12 a x d x = 4 π 2 3 a ∫ 0 a x 1 2 a + 3 x d x = 2 π 3 a ∫ 0 a a x 1 2 + 3 x 3 2 d x = 2 π 3 a 2 3 a x 3 2 + 6 5 x 5 2 0 a = 2 π 3 3 a 2 3 a 5 2 + 6 5 a 5 2 = 2 π 3 3 2 3 + 6 5 a 2 = 2 π 3 3 28 15 a 2 = 56 π 3 a 2 45

Resposta

  1. S = π 3 a 2
  2. S = 56 π 3 a 2 45
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região delimitada pelas curvas, e visualmente estime a localização do centroide. A seguir, calcule as coordenadas exatas do centroide. 25 .y = 4 - x 2 , y = 0
40 - Conforme visto no Exercício 39, o centroide do semicírculo y = a 2 - x 2 está no ponto ( 0,2 a π ). Determine a área da superfície gerada pela rotação do semicírculo em torno da reta a = y .
39 - Use o teorema de Pappus para área de superfície e o fato de que a área de superfície de uma esfera de raio a é 4 π a 2 para determinar o centroide do semicírculo y = a 2 - x 2
Nos Exercícios 45 e 46, use um teorema de Pappus para determinar o centroide do triângulo dado. Use o fato de que o volume de um cone de raio r e altura h é V = 1 3 π r 3 h .
38 - Use os teoremas de Pappus para determinar a área de superfície lateral e o volume e de um cone circular reto.