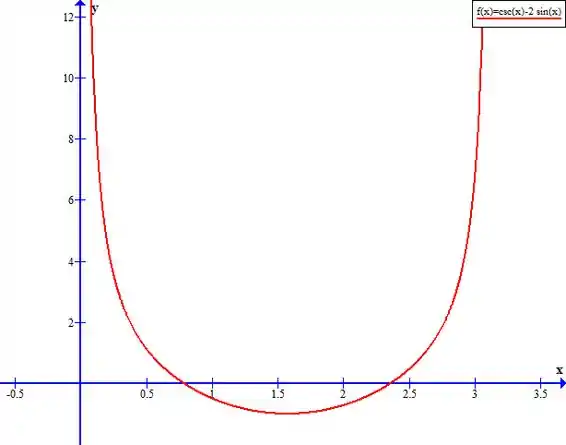
Use os guias desta seção para traçar a curva.
Passo 1
Fala aeee
Nessa questão temos a função
Definida para
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
E se há simetria ímpar, isso é:
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Passo 2
Bom pessoal, nesta seção nos é dado um guia para seguir que ajuda a traçar a curva de uma função.
Vamos segui-lo:
O domínio foi dado pelo enunciado:
Descobrir as interceptações da curva nos eixos y e x.
O intercepto ocorre quando temos:
A cossecante é o , logo:
Resolvendo temos:
Logo, as raízes dentro do intervalo que é são:
Para ver o intercepto , vemos o que ocorre em . No entanto não está definida para nossa função. E de fato não teria como estar definido, pois:
De forma que em , teríamos:
E a divisão por zero não é definida.
Checando simetria par:
Temos que , pois o seno é uma função par, logo:
Checando simetria ímpar:
Portanto, a função é impar e por periódica por ser trigonométrica. Entretanto, o domínio só esta definido para . Portanto a informação de simetria não servirá.
Para encontrar assíntotas, temos que checar a existência de limites.
Assíntotas Horizontais:
Como o domínio da função está definido apenas para um intervalo fechado , então não haverá assíntotas horizontais.
Para checar as assíntotas verticais, temos que analisar a função quando o denominador tende a zero:
Essa é uma indeterminação. Para resolvê-la, vamos realizar a subtração:
Substituindo o limite, temos:
No outro extremo do intervalo, temos:
Que também é uma indeterminação.
Substituindo o limite, temos:
Portanto haverá assíntotas verticais em
Passo 3
Intervalos crescentes e decrescentes. Temos que analisar a primeira derivada da função, onde:
Vamos lá:
Usando a derivada da cossecante tabelada e a derivada do seno:
Daí temos:
Resolvendo, temos:
Fatorando:
Avaliando o sinal dessa derivada, temos:
O fator é sempre positivo.
O fator é sempre positivo.
O fator é positivo quando:
Como está dentro do intervalo , temos então que o cosseno só é positivo no intervalo:
Como tudo isso está multiplicado por um fator , temos que quando:
Ou seja, no intervalo , temos e a função é decrescente.
Da mesma forma,no intervalo , temos e a função é crescente.
Por conta disso, o ponto é um ponto de extremo.
Como a função decrescia antes dele e depois dele ela cresce, temos que:
É um ponto de mínimo.
E
Passo 4
Para analisar a concavidade da função e achar seus intervalos, devemos usar a segunda derivada da função.
Pontos de inflexão ocorrem na mudança de concavidade.
A nossa função é:
Usando a derivada da cotangente, da cossecante e do cosseno:
Aplicando na nossa derivada, e usando a regra do produto, temos:
Temos que analisar dentro do domínio
Esta função sempre será maior que zero no intervalo do domínio, pois o seno será sempre positivo e o cosseno está ao quadrado. Logo:
Não há portanto pontos de inflexão.
Passo 5
Fazendo o nosso esboço reunindo as informações encontradas, temos:
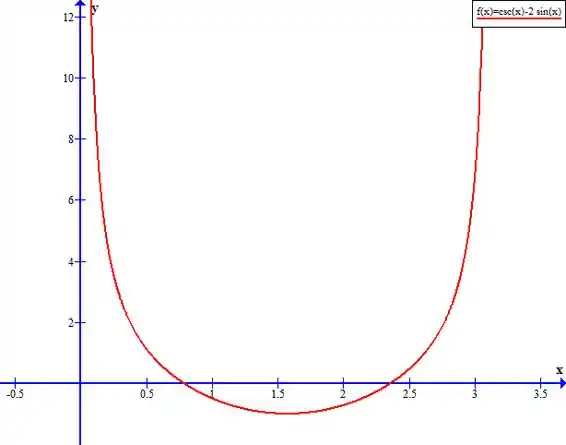
Resposta