Encontre a equação da assíntota obliqua. Não esboce a curva

Armando a nossa divisão temos:

Pegamos o primeiro termo do dividendo que é e dividimos pelo primeiro termo do divisor que é :

Esse valor vai lá pro quociente:

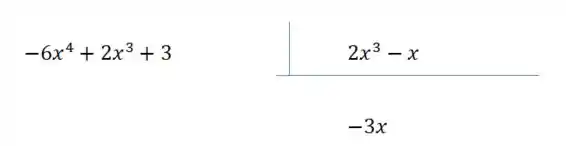
Agora multiplicamos o pelo divisor e trazemos ele com sinal trocado:

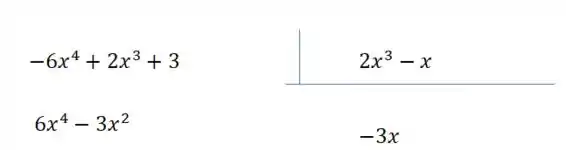
Agora somamos o dividendo por esses termos que trouxemos e obtemos então:

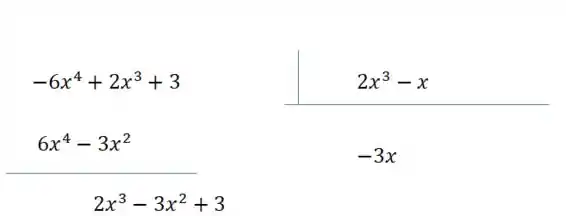
Repetimos então a operação, agora usando o que é o primeiro termo do dividendo:

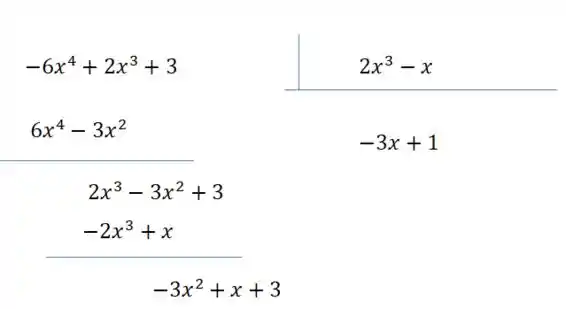
E agora nós paramos a conta, pois o dividendo possui um grau menor que o divisor. Dessa forma, encontramos o quociente e o resto

Nossa função é:

Podemos reescrevê-la como:

Perceba que quando tende a infinito, essa função tende a :

E com tendendo a infinito vale , logo:

Ou seja, quando vai para infinito, a função se comporta como essa reta, logo essa é a nossa assíntota oblíqua.

A assíntota obliqua vale então: