Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 15
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá as curvas:
Vamos esboçar a região delimitada por essas curvas. Temos duas funções exponenciais positivas e a reta .
Podemos calcular a intersecção dessas curvas e os valores de :
Então, o nosso gráfico fica assim:
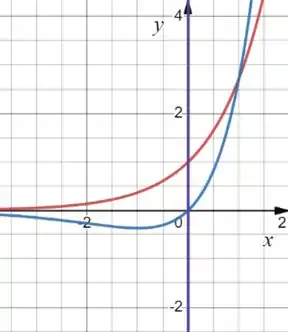
Onde a curva vermelha é , de azul é e a reta roxa é . O próximo passo vai ser calcular essa areazinha de verde:
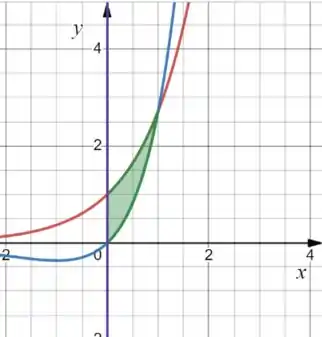
Passo 2
Agora vamos montar a integral! A área que vamos calcular vai ser dada pela subtração entre a curva vermelha e a curva azul e os limites de integração serão, no lado direito o ponto de intersecção entre as curvas e do lado esquerdo . Temos então:
Resolvendo essa integral:
Então,
Prontinho!
Resposta
Exercícios de Livros Relacionados
Use o teorema de Pappus para encontrar o volume de uma esfera com um raio de r unidades.
Prove a distância do centróide de um triângulo é igual a um terço da altura daquele lado.
Seja R a região limitada pelo semicrículo y = r 2 - x 2 e o eixo x. Use o teorema de Pappus para encontrar o momento de R em relação à reta y = - r .
Seja R a região limitada pelas curvas y = f 1 x e y = f 2 ( x ) . Se A for a medida da área de R e y - for a coordenada do centróide de R , prove que a medida do volume V do sólido de revolução obtido
Se o centróide da região limitada pela parábola y 2 = 4 p x e pela reta x = a estiver no ponto ( p , 0 ) , ache o valor de a .