Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 17

Esboce a região delimitada pelas curvas indicadas e encontre sua área.

x = 2 y 2 , x = 4 + y 2

Passo 1

Opa, bora resolver esse problema! O enunciado nos dá as curvas:

x = 2 y 2 , x = 4 + y 2

Temos em mãos duas parábolas em função de x . Ambas tem a concavidade pra “cima”, nesse caso como estamos analisando o y a concavidade vai ser na verdade pra direita!

Pra achar os pontos de intersecção fazemos:

2 y 2 = 4 + y 2

y 2 = 4

y = ± 2

Além disso precisamos calcular as raízes de cada curva:

x = 2 y 2 → y = x 2

x = 0

Agora a outra:

x = 4 + y 2 → y = x - 4

x = 4

Agora sim, conseguimos esboçar:

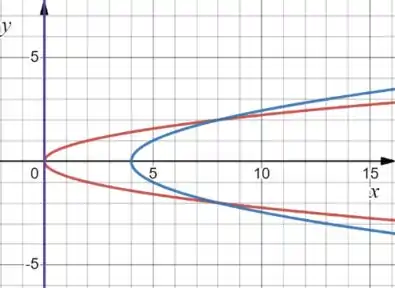
Onde a curva azul é x = 4 + y 2 e a curva vermelha é   x = 2 y 2 .

Passo 2

A área que a gente quer calcular é essazinha de verde:

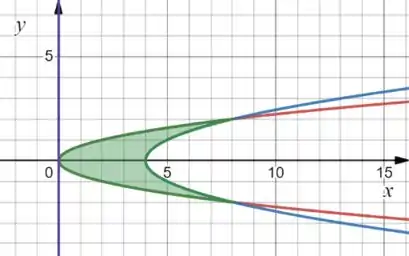
Passo 3

Agora vamos montar a integral! A área que vamos calcular vai ser dada pela subtração entre a curva vermelha e a curva azul e os limites de integração serão os pontos de intersecção que calculamos acima. Temos então:

A = ∫ a b f x - g x d x

A = ∫ - 2 2 ( 4 + y 2 ) - 2 y 2 d y

Simplificando:

A = ∫ - 2 2 ( 4 - y 2 ) d y

Essa integral pode ser dividida em duas partes, pois os intervalos de integração são iguais, logo:

A = 2 ∫ 0 2 4 - y 2 d y

Resolvendo essa integral:

A = 2 4 y - y 3 3 0 2

A = 2 4 ( 2 ) - ( 2 ) 3 3 - [ 0 ]

Então,

A = 2 8 - 8 3

A = 32 3

Prontinho!

Resposta

A = 32 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (11) A parábola y = x ³ ³ e a reta y = 4 x mo primeiro quadrante.
Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (14) A parábola y = x 2 e y = x ³ ³.
Use o teorema de Pappus para encontrar o centróide da região limitada por um semicírculo e seu diâmetro.
Use o teorema de Pappus para encontrar o volume do toro (da forma de uma câmara de ar) gerado com a revolução de um círculo com um raio de r unidades em torno de uma reta em seu plano, a uma distância
Use o teorema de Pappus para encontrar o volume de um cone circular reto com raio da base r unidades e altura h unidades.