Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.3 - Ex. 7
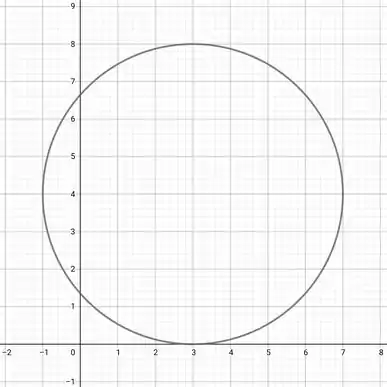
Ache o centro e o raio da circunferência e desenhe um esboço do gráfico:
Passo 1
Para encontrar o centro e o raio de uma circunferência a partir de sua equação geral, primeiro devemos escrevê-la na forma centro-raio e comparar com a fórmula , em que são as coordenadas do centro e r é o raio. Para isso, vamos completar quadrados.
(Lembrando: trinômio quadrado perfeito: )
Passo 2
Para completar quadrados, observamos a parcela com a variável na primeira potência. Dividimos então o coeficiente dessa variável por 2 e o resultado nós elevamos ao quadrado e somamos dos dois lados da equação.
Assim , e .
Resposta
Centro:
Raio: .
Exercícios de Livros Relacionados
Ache uma equação da circunferência com centro em C e raio r. Escreva a equação na forma centro-raio e na forma geral. C - 5 ,- 12 ,r = 3
Ache uma equação da circunferência que satisfaça as condições: Passa pelos três pontos ( 2 ,8 ) , ( 7 ,3 ) e ( - 2 ,0 ) .
Determine se o gráfico é uma circunferência, um ponto ou um conjunto vazio. x 2 + y 2 - 2 ⋅ x + 10 ⋅ y + 19 = 0
Determine se o gráfico é uma circunferência, um ponto ou um conjunto vazio. 4 x 2 + 4 y 2 + 24 x - 4 y + 1 = 0 x 2 + y 2 + 6 x - y + 1 4 = 0 x 2 + 6 x + 9 - 9 + y 2 - y + 1 4 = 0 x + 3 2 + y + 1 2 2 =
Determine se o gráfico é uma circunferência, um ponto ou um conjunto vazio. x 2 + y 2 + 2 ⋅ x - 4 ⋅ y + 5 = 0