Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.2 - Ex. 6
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos.
Passo 1
A questão pede para encontrar as principais características da elipse . Note que neste caso não temos termos de primeiro grau, então o centro da elipse será a origem . Assim, basta dividir a equação por :
Ou ainda,
Portanto,
Como o maior termo está sobre , temos que os focos estarão sobre o eixo e:
Assim, o comprimento do eixo menor será
E os vértices estarão em
Já as extremidades do eixo menor estarão no eixo :
Passo 2
Para acharmos os focos, temos que
Assim,
Portanto, os focos serão
Passo 3
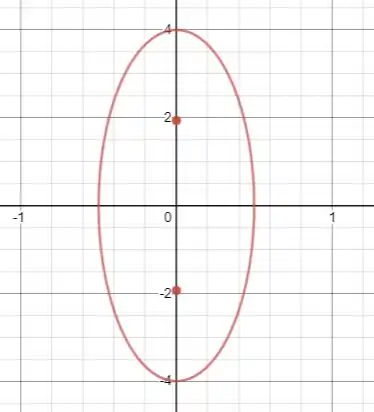
Um esboço da elipse é mostrado a seguir:
Resposta
Centro:
Vértices:
Extremidades do eixo menor:
Focos:
Exercícios de Livros Relacionados
As elipses E e E ' , de parâmetros geométricos a , b , c e a ' , b ' , c ' , têm centro O e focos em um dos eixos coordenados. Sendo a ' = k a e b ' = k b , prove que c ' = k c e que P = x , y pertenc
Pela primeira Lei de Kepler, a trajetória da Terra é elíptica e o Sol ocupa a posição de um de seus focos. Calcule o periélio e o afélio da Terra (que são, respectivamente, a menor e a maior distância
Em cada caso, determine os vértices, os focos, e as medidas dos eixos maior e menor da elipse. E : 16 x 2 + 25 y 2 = 400 E : x 2 + 9 y 2 = 9 E : 50 - y 2 - 2 x 2 = 0 E : 3 x 2 + 4 y 2 - 12 = 0 .
Em cada caso, determine os vértices, os focos, e as medidas dos eixos maior e menor da elipse. E : 16 x 2 + 25 y 2 = 400 E : x 2 + 9 y 2 = 9 E : 50 - y 2 - 2 x 2 = 0 E : 3 x 2 + 4 y 2 - 12 = 0 .
Sendo X = x , y um ponto de E : x 2 b 2 + y 2 a 2 = 1 e d 1 e d 2 as distâncias de X aos focos, calcule? d 1 e d 2 em função de y ;Os valores máximo e mínimo de d 1 e d 2 ; em que pontos ocorrem?