Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.2 - Ex. 39
Uma mulher está andando com uma velocidade de ao longo de um diâmetro de um pátio circular. Uma luz no extremo de um diâmetro perpendicular ao seu caminho projeta sua sombra sobre a parede circular do pátio. Com que velocidade a sombra estará se movendo ao longo da parede quando a distância da mulher ao centro do pátio for ? ( é o raio do pátio).
Passo 1
Um esquema para ilustrar o problema é mostrado a seguir:
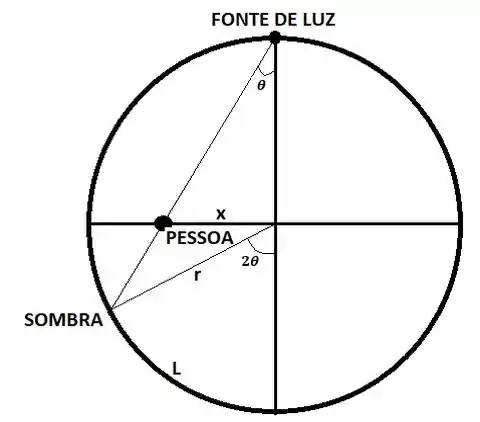
Temos que representa a distância da mulher até o centro do pátio e representa o comprimento do arco que será descrito pela sombra da mulher. Por simplicidade, vamos supor que a mulher se move para a esquerda. Assim, a velocidade dela será representada por , enquanto a velocidade da sombra será , onde todas as derivadas são tomadas com relação ao tempo.
Do triângulo retângulo com catetos e , temos que
Além disso, como um comprimento de um arco é o arco em radianos multiplicado pelo raio, temos que
Passo 2
Derivando as duas equações e lembrando que é constante:
Substituindo a primeira equação na segunda:
Agora só falta substituir e :
Portanto, temos que a velocidade com que a sombra se desloca é .