Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 106

Ache o centroide da região limitada pelo laço da curva y 2 = x 2 - x 3 .

Passo 1

A questão pede para acharmos o centroide da região limitada pelo laço da curva y 2 = x 2 - x 3 . Um esboço do gráfico da curva é dado a seguir:

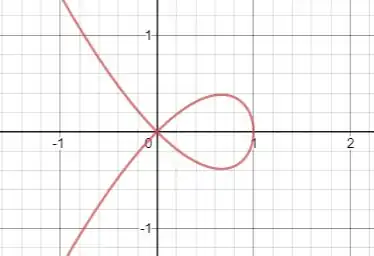
Note que por simetria, a coordenada y do centro de massa será 0 , isto é

y - = 0

Isso ocorre porque o eixo x é o eixo de simetria da região. Além disso, como a região acima do eixo x é exatamente igual a região abaixo, podemos considerar apenas a parte de cima para achar o centro de massa!

Vamos isolar y como função de x :

y 2 = x 2 1 - x ⇒ y = ± x   1 - x = x 1 - x

Escolhemos o sinal positivo pois vamos usar apenas a parte acima do eixo x ( y ≥ 0 ). A coordenada x do centro de massa de uma região limitada por uma curva do tipo y = f ( x ) e o eixo x é dado por

x - = 1 A ∫ x   f x   d x ,

onde A é a área da região:

A = ∫ f x   d x

Passo 2

Vamos calcular primeiro a área:

A = ∫ 0 1 x 1 - x   d x

Vamos fazer a substituição t = 1 - x ⇒ d t = - d x e x = 1 - t :

A = ∫ 1 0 1 - t t   - d t = ∫ 0 1 1 - t   t   d t

Assim, podemos calcular a integral:

A = ∫ 0 1 t 1 2 - t 3 2   d t = 2 3 t 3 2 - 2 5 t 5 2 0 1

Portanto,

A = 2 3 - 2 5 = 4 15

Passo 3

Agora que temos a área, podemos escrever:

x - = 1 A ∫ x   f x   d x = 15 4 ∫ 0 1 x 2 1 - x   d x

Vamos fazer a mesma substituição do passo anterior: t = 1 - x :

x - = 15 4 ∫ 0 1 1 - t 2 t   d t = 15 4 ∫ 0 1 t 2 - 2 t + 1 t   d t

Assim,

x - = 15 4 ∫ 0 1 t 5 2 - 2 t 3 2 + t 1 2   d t = 15 4 2 7 t 7 2 - 4 5 t 5 2 + 2 3 t 3 2 0 1

Portanto,

x - = 15 4 2 7 - 4 5 + 2 3 = 15 4 30 - 84 + 70 105 = 15 4 ⋅ 16 105 = 4 7

Desta forma, as coordenadas do centroide serão

4 7 ,   0

Resposta

4 7 ,   0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o centro de massa do gráfico da função dada f x = x 2 , - 1 2 ≤ x ≤ 1 2
(Teorema de Papus.) Considere o conjunto A = { x , y ∈ R a ≤ x ≤ b ,f x ≤ y ≤ g ( x ) } Onde f e g são supostas contínuas em [ a , b ] e 0 ≤ f x ≤ g x em [a,b]. Mostre que o volume do sólido, obtido p
Sejam f e g continuas em [a,b], com α ≤ f xg x e ma , b onde α é um real dado. Seja o conjunto A = { x , y ∈ R a ≤ x ≤ b , f x ≤ y ≤ g ( x ) } Mostre que o volume do sólido obtido, pela rotação em tor
Calcule o volume do sólido obtido pela rotação do círculo x 2 + y - 2 2 ≤ 1 em torno do eixox
Calcule o volume do sólido obtido pela rotação do círculo x 2 + y - 2 2 ≤ 1 em torno da reta y = 1