Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 2

Ache o volume do sólido de revolução descrito pelo método do invólucro cilíndrico quando a região dada da figura for rotacionada em torno da reta indicada. Uma equação da curva na figura é y 2 = x 3 .

2. Sólido obtido rotacionando O A C em torno da reta A C .

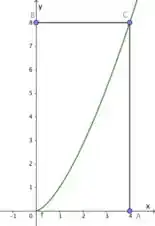
Passo 1

Pessoal, a região rotacionada é a que está abaixo da curva, ok? E como vai ser a rotação em torno da reta x = 4 usando o método do invólucro cilíndrico e temos uma função na variável x , está perfeito para usar o método, apenas precisamos botar o y isolado.

y 2 = x 3 →     y = x 3 2

Agora para resolver, a primeira coisa a se fazer é lembrar a fórmula que calcula o volume do sólido obtido em um intervalo [ a , b ] .

V = 2 π ∫ a b r x h ( x ) d x

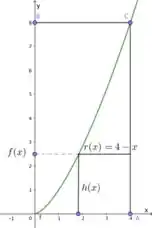
Como a rotação vai ser em torno da reta x = 4 , a função raio será r x = 4 - x , como vocês podem ver na imagem acima. Já a função altura h x será f x = x 3 2 . O intervalo de integração será da reta x = 0 a reta x = 4 . Sendo assim, o volume é dado por:

V = 2 π ∫ 0 4 ( 4 - x ) x 3 2 d x = 2 π ∫ 0 4 ( 4 x 3 2 - x 3 2 + 1 ) d x = 2 π ∫ 0 4 ( 4 x 3 2 - x 5 2 ) d x

Passo 2

Já podemos resolver a integral. Sabemos da integral definida que:

∫ a b f x d x = F b - F a

Em que F é uma primitiva de f .

Devemos lembrar também que:

∫ x n d x = x n + 1 n + 1 + C           n ≠ - 1

Dessa forma,

V = 2 π ∫ 0 4 ( 4 x 3 2 - x 5 2 ) d x = 2 π 4 x 3 2 + 1 3 2 + 1 - x 5 2 + 1 5 2 + 1 0 4

= 2 π 4 4 5 2 5 2 - ( 4 ) 7 2 7 2 - 0 - 0 = 4 π 4 2 2 5 2 5 - ( 2 2 ) 7 2 7

= 4 π 4 ⋅ 2 5 5 - 2 7 7 = 4 π 128 5 - 128 7 = 4 π 7 ⋅ 128 - 5 ⋅ 128 35

= 4 π 2 ⋅ 128 35 = 1024 π 35   u . v

Logo, o volume é V = 1024 π 35   u . v .

Resposta

V = 1024 π 35   u . v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. x = 1 + y 2 ,
Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo y da região limitada pelas curvas dadas. Esboce a região e uma casca típica. y = e - x 2 ,y = 0 , x = 0 ,x
Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo y da região limitada pelas curvas dadas. Esboce a região e uma casca típica. y = x 2 ,y = 6 x - 2 x ² ²
Encontre o volume do sólido obtido quando a região sob a curva y = x 4 - x 2 , 0 ≤ x ≤ 2 é girada em torno do eixo y .
Use cascas cilíndricas para encontrar o volume do sólido.Um cone circular reto de altura h e base com raio r .