Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 3.1 - Ex. 40
Ache . Compare os gráficos de e e use-os para explicar por que sua resposta é razoável.
Passo 1
Nesta questão precisamos encontrar e esboçar o gráfico tanto de como de . Em seguida, devemos comparar os gráficos e dizer se eles são consistentes entre si. Vale lembrar que onde a derivada é positiva, a função é crescente, onde ela se anula a função deve ter uma tangente horizontal, e assim por diante...
Passo 2
Derivando a função, temos que
Passo 3
Em vermelho esboçamos o gráfico de e em azul o de :
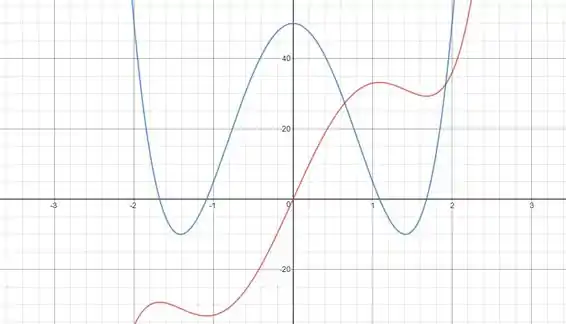
Note que nos pontos que a curva vermelha tem tangente horizontal, a curva azul cruza o eixo . Além disso, nos únicos trechos que a curva azula é negativa, a curva vermelha é descrescente.
Resposta
e esboço de gráfico.
Exercícios de Livros Relacionados
Use os guias desta seção para traçar a curva. y = 1 x 2 - 4
Use os guias desta seção para traçar a curva. y = sin x + 3 cos x , - 2 π ≤ x ≤ 2 π
Use o roteiro dessa seção para esboçar a curva. y = x 3 + 6 x 2 + 9 x
10. Use o roteiro desta seção para esboçar a curva: y = x 2 + 5 25 - x ² ²
Use os guias desta seção para traçar a curva. y = 1 x + ln x