Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 48
Ache, pelo corte, o volume de um tetraedro com três faces mutuamente perpendiculares e três arestas mutuamente perpendiculares cujos comprimentos são , e unidades.
Passo 1
A questão pede para acharmos o volume do tetraedro trirretângulo com arestas medindo , e . Vamos posicionar essas três arestas mutuamente perpendiculares nos eixos , e :
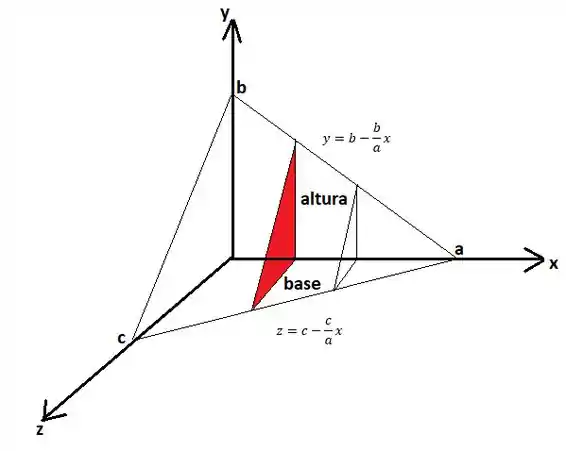
Para achar esse volume, precisamos escrever uma expressão em função de para a área de uma secção (fatia) e depois integrar essa área em de até . Para isso nós precisamos achar as equações da reta no plano e da reta no plano . Essas equações nos darão a altura e a base da seção transversal que iremos integrar!
No plano , a reta passa pelos pontos e , assim, sua equação deve ser
Já no plano , ela passa pelos pontos e , de modo que
Temos então que
Desta forma, a área da secção transversal (que é um triângulo) será
Para acharmos o volume, basta integrar:
Passo 2
Desta forma, temos que
Fazendo a integração:
Portanto,