Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 53

Encontre o volume do sólido S descrito. Um tetraedro com três faces perpendiculares entre si e as três arestas perpendiculares entre si com comprimento de 3 c m , 4 c m e 5 c m .

Passo 1

Queremos encontrar o volume de um tetraedro com três faces perpendiculares entre si e as três arestas perpendiculares entre si com comprimento de 3 c m , 4 c m e 5 c m .

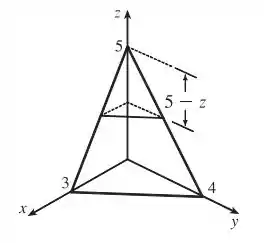
Fazendo um corte transversal de altura z temos um triângulo similar à base, então nós iremos multiplicar as arestas da base triangular, 3 e 4 , por uma fator de proporcionalidade. A altura total do triângulo é igual a h T = 5 , podemos escrever esse fator como:

h T - z h T = 5 - z 5

Passo 2

Podemos calcular a área da base do triângulo pequeno, fazendo:

A z = 1 2 a 1 a 2

Onde a 1 e a 2 são as arestas que vamos multiplicar pela constante de proporcionalidade:

a 1 = 3   5 - z 5

a 2 = 4   5 - z 5

Substituindo, temos:

A z = 1 2 3 5 - z 5   4 5 - z 5 = 6 1 - z 5 ²  

Passo 3

Tendo a área, podemos achar o volume fazendo a seguinte integração:

V = ∫ 0 5 A z d z = 6 ∫ 0 5 1 - z 5 2 d z = 6 ∫ 1 0 u 2 - 5 d u

u = 1 - z 5

d u = - 1 5 d z

V = - 30 1 3 u 3 1 0 = - 30 - 1 3 = 10 c m ³

Resposta

V = 10 c m ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-10, determine os volumes dos sólidos.2- O sólido está situado entre planos perpendiculares ao eixo x em x = - 1 e x = 1 .As seções transversais perpendiculares ao eixo x são discos ci
Nos Exercícios 1-10, determine os volumes dos sólidos.7- A base de um sólido é a região limitada pelos gráficos de y = 3 x , y = 6 e x = 0 . As seções transversais perpendiculares ao eixo x sãoRetângu
Nos Exercícios 1-10, determine os volumes dos sólidos.7- A base de um sólido é a região limitada pelos gráficos de y = 3 x , y = 6 e x = 0 . As seções transversais perpendiculares ao eixo x sãoRetângu
Nos Exercícios 1-10, determine os volumes dos sólidos.4- O sólido está situado entre os planos perpendiculares ao eixo x em x = - 1 e x = 1 . As seções transversais perpendiculares ao eixo x entre ess
Nos Exercícios 1-10, determine os volumes dos sólidos.8- A base de um sólido é a região limitada pelos gráficos de y = x e y = x / 2 . As seções transversais perpendiculares ao eixo x são: b) semicírc