Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 21
Ache o domínio da função e diga se é contínua nos intervalos:
Intervalos:
Passo 1
Para encontrar o domínio de uma função, devemos lembrar que não podemos dividir por 0. Logo, temos nossa restrição sendo o denominador , ou seja, .
O domínio é (os reais exceto o 1)
Passo 2
Antes de determinar a continuidade em cada intervalo, repare que a nossa função f tem quase a mesma expressão no numerador e no denominador, a diferença está apenas no módulo! Então vamos mudar um pouco essa função para facilitar o entendimento:
Se , pois módulo é sempre um número postivo.
Se
Assim, posso escrever
Logo, temos duas semirretas constantes com um salto no ponto , como vemos no gráfico:
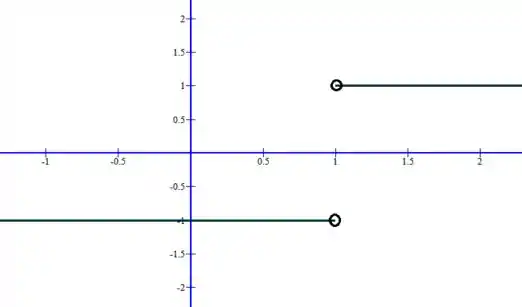
Assim, basta ver se o número 1 pertence ou não ao intervalo para determinar a continuidade.
Passo 3
Intervalo não pertence, então é contínua.
Intervalo pertence, então não é contínua.
Intervalo pertence, então não é contínua.
Intervalo pertence, então não é contínua.
Intervalo não pertence, então é contínua.
Resposta
É contínua nos intervalos:
Não é contínua nos intervalos: