Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 22
Ache o domínio da função e diga se é contínua nos intervalos:
Intervalos:
Passo 1
Para encontrar o domínio de uma função, devemos verificar se há restrições nas equações. Mas nota-se que todas as equações são polinômios do primeiro grau (retas), ou seja, são bem definidas pra qualquer número real que você escolha!
Assim, nosso domínio será (todos os reais)
Passo 2
Antes de determinar a continuidade da função nos intervalos dados, note que a função é definida por 3 retas e todas as retas são contínuas (se olhadas sozinhas) por serem polinomiais (Você sempre consegue desenhar uma reta sem tirar o lápis do papel). Porém, a possível descontinuidade da função pode estar no encontro dessas retas, como por exemplo:
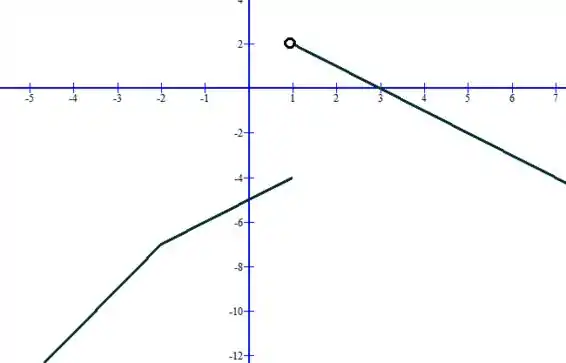
Temos nesse gráfico duas retas que se encontram e formam uma “ponta” e outro que não os encontra. Nesse caso, a função só é descontínua no “desencontro”.
Note que esse é exatamente o esboço do gráfico da função , o que nos leva a concluir que a continuidade da função vai depender do número 1 pertencer ou não ao intervalo.
Passo 3
Intervalo não pertence, então é contínua.
Intervalo pertence, então é descontínua.
Intervalo não pertence, então é contínua.
Intervalo não pertence, então é contínua.
Intervalo não pertence, então é contínua
Resposta
É contínua nos intervalos:
Não é contínua no intervalo: