Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.2 - Ex. 26
Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.
Um foco em , um vértice em , e centro sobre o eixo .
Passo 1
A questão pede a equação da elipse com um foco em , um vértice em e cujo centro está sobre o eixo .
Se o centro está sobre o eixo , ele é do tipo ). Além disso, note que tanto o foco como o vértice estão sobre a reta , que é uma reta vertical. Assim, o eixo principal da elipse é vertical e sua equação será do tipo
Notemos também que o centro da elipse deve estar sobre o eixo principal dela, cuja equação é . Assim, o ponto deve pertencer a essa reta, de modo que .
A distância do foco até o centro será e a do vértice até o centro será .
Passo 2
Para termos a equação completa da elipse só falta achar :
Assim, a equação da elipse será
Passo 3
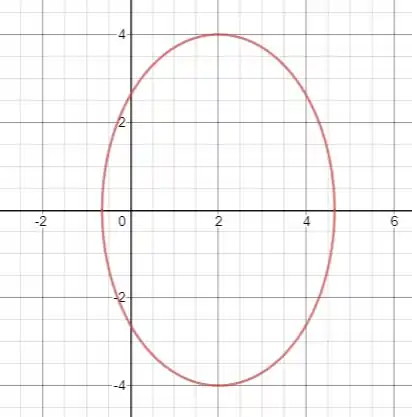
O esboço da elipse é mostrado a seguir:
