Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 26
Em cada um dos Problemas de 20 a 27, obter uma equação da elipse que satisfaça as condições dadas.
Centro , um foco e tangente ao eixo dos y
Passo 1
O enunciado diz que ele é tangente ao eixo dos y, então ele só pode tocar em apenas um ponto, então o único ponto possível é se ele for um vértice, então ele precisa ter a forma
Maaas como ele está no eixo dos y, temos que , então nosso ponto é
Passo 2
Como temos que esse ponto é um vértice, podemos encontrar quem é , vai ser a distancia do centro ao ponto, como o centro é e o ponto é o
E irá acompanhar
Agora vamos achar quem são os outros coeficientes, o enunciado diz que temos um foco em , como é a distancia do centro ao foco, temos que
E para achar , vamos utilizar aquela famosa relação do triangulo retângulo, se você não lembra de onde sai esse triangulo, vou te mostrar aqui:
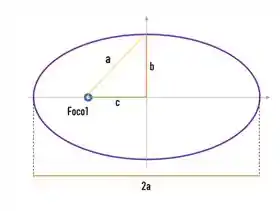
Então temos que
Passo 3
Agora que temos nossos coeficientes e sabemos quem é o nosso centro, vamos colocar na equação da elipse que é assim:
Ajeitando isso dai ficamos com