Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 18
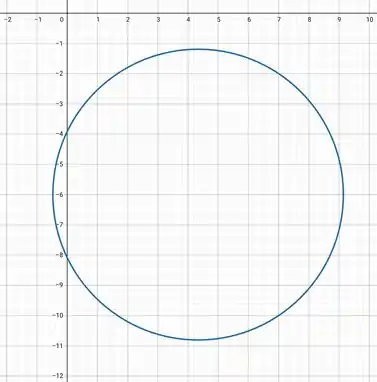
Ache uma equação que seja satisfeita pelas coordenadas de qualquer ponto cuja distância ao ponto seja o dobro da distância a . Faça um esboço do seu gráfico.
Passo 1
Para encontrar todos os pontos cuja distância ao ponto seja duas vezes a distância ao ponto , precisamos lembrar da fórmula de distância entre dois pontos:
Passo 2
Passo 3
Temos uma equação, mas ela não é ideal para construirmos um gráfico pois não se parece com nenhuma que conhecemos. Logo, completaremos quadrados para tentar transformá-la em algo que conheçamos.
Passo 4
Pela equação acima, o conjunto de pontos procurado é uma circunferência de centro e raio .
Resposta
Exercícios de Livros Relacionados
23. Calcular o valor de m para que sejam coplanares as seguintes retas r : y = 2 x + 3 z = 3 x - 1 e s : x - 1 2 = y - 1 = z m r : x = - 1 y = - 3 e s : y = 4 x - m z = x r : x - m m = y - 4 - 3 ; z =
23. Calcular o valor de m para que sejam coplanares as seguintes retas r : y = 2 x + 3 z = 3 x - 1 e s : x - 1 2 = y - 1 = z m r : x = - 1 y = - 3 e s : y = 4 x - m z = x r : x - m m = y - 4 - 3 ; z =
Determinar as equações paramétricas da reta que passa pelos pontos A e B nos seguintes casos:d) A 0 , 0,0 ; B ( 0,1 , 0 ) .
Dada a reta x = 2 + t y = 3 - t z = - 4 + 2 t Determinar o ponto r tal que c) a cota seja o quádruplo da abscissa.
Determinar as equações paramétricas da reta que passa pelos pontos A e B nos seguintes casos:b) A 3,1 , 4 ; B ( 3 , - 2,2 ) .