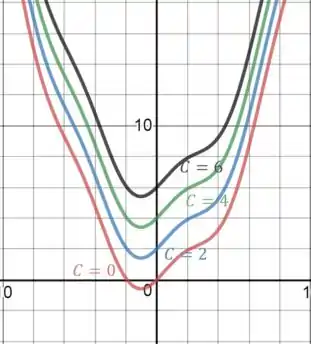
Ache a integral indefinida geral. Ilustre fazendo o gráfico de vários membros da família na mesma tela.

Bom pessoal, nessa questão temos que resolver a seguinte integral:

Para isso, vamos usar a propriedade de que a integra da soma/subtração é a soma/subtração de integrais:

E também vamos usar a propriedade de que uma constante pode sair da integral:

E para resolver cada integral vamos usar a ideia de antiderivada.

Aqui temos a potência de , e a regra da antiderivada para a potência de é:

E também temos a função cosseno. A antiderivada do cosseno é o seno:

E por se tratar de uma integral indefinida, temos que somar a constante no final!

O enunciado também pede para que a gente plote numa mesma janela diversas funções dessa família de função, isso é, plotar o resultado para valores de diferentes.