Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.5 - Ex. 30
Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado.
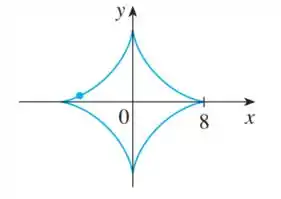
, (astroide)
Passo 1
Eaee, belezinha?? Bom... O enunciado pede a equação da reta tangente à uma curva dada por:
No ponto .
Assim, para acharmos da equação de uma reta, precisamos de duas informações: um ponto em que ela passa (o enunciado já forneceu) e sua inclinação.
Assim, podemos usar a equação da reta na forma ponto-inclinação:
Onde representa a inclinação (ou coeficiente angular da reta) e , os pontos dados.
Para a reta tangente, será a derivada de com relação a , isto é, no ponto de tangência.
Assim, para encontrar , devemos derivar implicitamente a equação fornecida.
Agora bora lá!! 😉
Passo 2
Derivando a equação implicitamente com relação a :
No caso de derivar , se assemelha a aplicação da regra da cadeia:
Então,
Passo 3
Como o ponto de interesse é , devemos substituir e na equação encontrada no passo 2:
Como , então:
Assim,
Assim, o coeficiente angular da reta tangente será .
Passo 4
Agora basta substituir o ponto e a inclinação na equação da reta:
Entendeu direitinho?? Responde aee 😉