Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.8 - Ex. 31
Ache a região interior à elipse acima da parábola .
Passo 1
Então galera, se tivermos uma função do tipo e se unidades de área for a área da região , então teremos:
Oxe, que que isso significa? Sinceramente, nem eu sei muito bem, então vamos para um definição melhor, saca só:
Ok, agora sim ficou mais claro! No entanto, no nosso caso se trata de uma região entre duas funções. Sendo assim, teremos o seguinte:
No qual é a função superior e é a função inferior, belê?
Passo 2
Antes de tudo, vamos plotar esses gráficos aí em um plano cartesiano. Vale ressaltar que estaremos plotando em coordenadas e mesmo, sem ser em coordenadas cartesianas como deveria ser. No entanto, isso não será problema, os valores encontrados serão os mesmos!
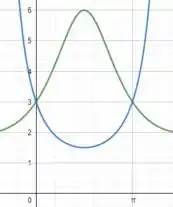
No qual a função em verde é e a função em azul é . Observando o gráfico, notamos que as funções se interceptam em e em , certo? No qual o formato desses pontos é . Como gráfico é simétrico em relação ao eixo , então podemos fazer:
Então galera, é mais fácil resolvermos essas integrais em termos do cosseno e não em termos do seno. Para mudarmos isso, vamos fazer algumas substituições nada intuitivas, tudo bem? Temos que:
Que é algo definido da trigonometria mesmo. Ademais, temos que , então substituindo nas integrais, teremos:
Agora que vem a substituição relativamente complicada de se enxergar. Vamos utilizar aqui a substituição pela tangente do ângulo metade. Em outras palavras, vamos fazer:
E de acordo com a teoria dessa substituição, temos que:
Galera, esses valores não foram tirados do nada não, tá? Se tiverem alguma dúvida aqui, procurem por essa substituição, uma vez que em alguns casos, principalmente se tratando de coordenadas polares, ela passa a ser muito útil. Passando para a integral, teremos:
Passo 3
Ufa! Depois desse trabalhão, agora sim temos uma integral mais interessante de ser resolvida, por mais que ainda esteja mal escrita! Se fizermos as distributivas e simplificações, teremos a seguinte integral:
Para simplificar a visualização, vamos fazer:
Para vamos fazer a seguinte substituição: . Para modificarmos os intervalos de integração em função da substituição por , temos:
Utilizando trigonometria, teremos:
Para , temos:
Por fim, como , assim como definimos, então: