Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 74
Ache a região limitada pelas duas parábolas:
Passo 1
Primeiro passo é nós fazermos um esboço do que a gente tá trabalhando, para facilitar qualquer decisão tomada.
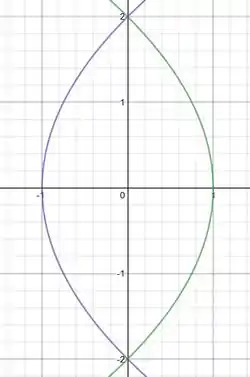
Em verde temos .
Para calcular a área, basta transformarmos nossa função em coordenadas cartesianas e a partir dai calcular a integral de apenas uma (dentro dos limites), já que elas são simétricas.
Passo 2
Vamos transformar somente essa equação , pois vamos usar ela como uma simetria da outra.
Integrando isso em x, temos que:
=
Passo 3
Agora basta multiplicar por 2, para pegar a área das duas assíntotas.
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 35 a 44, ache a equação cartesiana do gráfico dada a sua equação polar39. r 2 = θ
Nos exercícios de 25 a 34, ache a equação polar do gráfico dada a sua equação cartesiana 42. r 6 = r 2 c o s 2 θ
Nos exercícios de 35 a 44, ache a equação cartesiana do gráfico dada a sua equação polar 43 .r = 6 2 - 3 s e nθ
Nos Exercícios 13 a 20, o gráfico da equação dada é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o
Nos Exercícios 13 a 20, o gráfico da equação dada é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o