Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.2 - Ex. 4
a) Ache a soma de Riemann para , com seis termos, tomando como pontos amostrais os extremos direitos. (Dê sua resposta correta até a sexta casa decimal.) Explique o que representa a soma de Riemann com a ajuda de um esboço.
b) Repita a parte (a) tomando como pontos amostrais os pontos médios.
Passo 1
Opa! E aí, bora resolver essa questão?! O enunciado pede pra a gente calcular a soma de Riemann para essa função aqui:
No intervalo . Ou seja, queremos calcular:
Pra isso ele pede pra a gente subdividir o intervalo dado em subintervalos, ou seja e devemos considerar a extremidade direita de cada subintervalo pro nosso cálculo!
O próprio enunciado já diz que a gente deve resolver o problema pela soma de Riemann, pra isso a gente vai usar essa forma geral aqui:
Onde é dado por:
Como a gente vai pegar os pontos da extremidade esquerda de cada intervalo, temos então , que pode ser calculado por:
Na prática, pra fazer o exercício, vamos abrir a integral ali de cima e vamos ficar com:
Depois de fazer tudo isso, repetiremos o processo, mas usando como pontos amostrais os pontos médios.
Passo 2
(a) A soma de Riemann para uma função com 6 subintervalos (), com aproximação pelos extremos direitos, pode ser definida pelo seguinte somatório:
Temos , então dividindo nosso intervalo em 6, é:
E nossos ’s são: , , e , e . Esses são os pontos finais de cada intervalo. A soma de Riemann fica então:
Assim, vamos calcular cada uma dessas funções:
Assim:
Passo 3
Traçando o gráfico de , podemos representar os intervalos de tamanho e os valores da função nos finais do intervalo, formando retângulos.
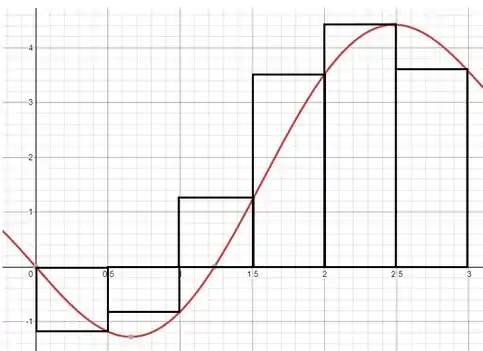
Como podemos ver, a soma de Riemann de uma função busca aproximar a área entre a curva e o eixo x (considerando que a parte abaixo do eixo tem área negativa), do mesmo modo que fazemos ao calcular a área de retângulos aproximantes.
Passo 4
(b) Agora fazemos novamente a soma de Riemann, mas tomamos como valor de a função nos pontos do meio dos intervalos, e não no final. Por exemplo, para o intervalo usamos e não como fizemos antes. A soma fica então:
E calculando cada uma das funções, teremos:
Assim,
E prontinho.