Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 68c
Ache todos os valores de t no intervalo de para os quais a equação dada é satisfeita:
c)
Passo 1
Queremos obter os ângulos (valores de t) no intervalo de que tenham sua tangente igual a .
Para começar vamos desenhar nosso circulo trigonométrico, cujo raio é igual a 1.
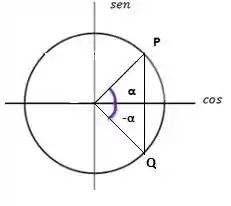
Se observarmos o círculo, os ângulos com medidas negativas (-α) possuem uma correspondente positiva (α), ou seja:
Analogamente:
Passo 2
Tendo isto em mente, podemos obter o valor de t pela tabela trigonométrica. Então:
Sendo assim:
Então:
Em radianos:
O termo negativo se refere à rotação do ângulo no sentido horário. Para obtermos no sentido anti-horário, basta subtrair do valor do ângulo total (2π). Então:
Resposta
Exercícios de Livros Relacionados
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da