Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 50

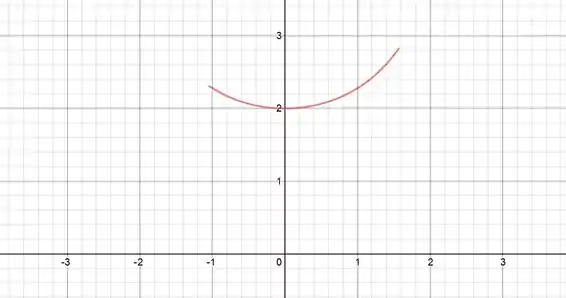
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos Exemplos 3 e 4 desta secção. Faça um esboço do gráfico da função no intervalo.

h x = 2 sec ⁡ 1 2 x ; - 1 3 π , 1 2 π

Passo 1

Vamos seguir um passo a passo tranquilo pra resolver esses problemas, da mesma forma que o livro faz nos exemplos 3 e 4 desta seção.

  1. Determinar a derivada da função.
  2. Fazer f ' x = 0 e depois encontrar os valores de x para os quais f ' x   não existe.
  3. Achar os valores de x que satisfazem as proposições acima e estão dentro do intervalo especificado.
  4. Dos valores encontrados, o menor vai ser o mínimo absoluto e o maior será o máximo absoluto do intervalo.
  5. Esboçar o gráfico utilizando os valores de máximo e mínimo que temos.

Vamo devagarinho que dá bom!

Passo 2

Antes de tudo vamos relembrar o gráfico da função sec ⁡ x :

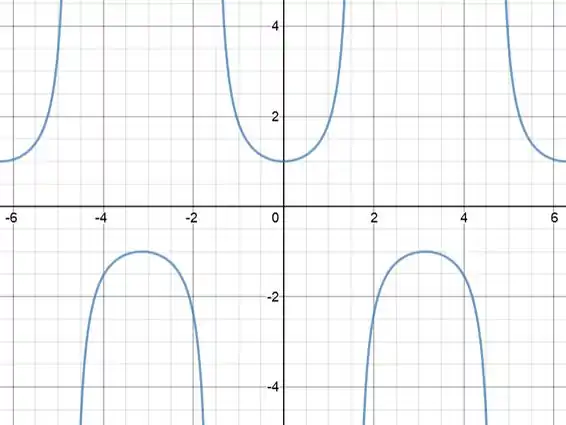
No intervalo especificado da questão, vamos ficar só com:

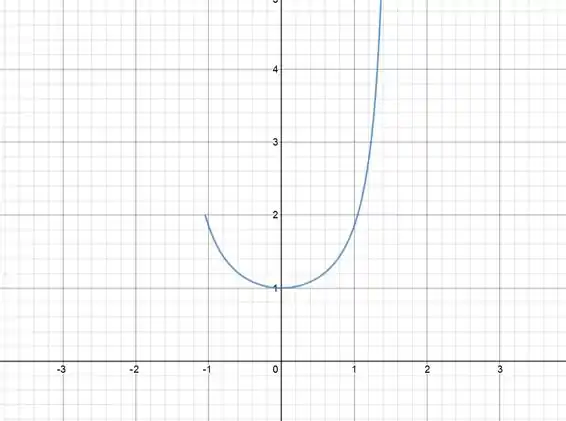
Mas a nossa função não é sec ⁡ x . Nós temos 2 sec ⁡ 1 2 x . A nossa função tem metade da frequência angular do que a função que temos o gráfico e ao invés de ter um mínimo em y = 1 , teremos um mínimo em y = 2 , desta forma:

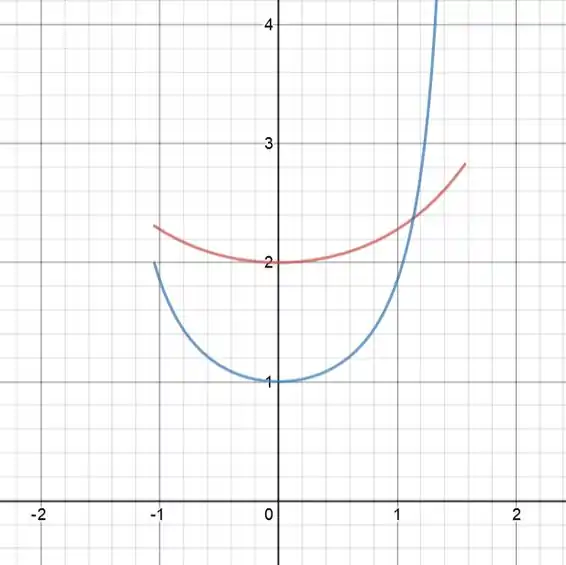
Em vermelho temos a nossa função e em azul temos a função sec ⁡ x . Vemos que a nossa função é continua nesse intervalo, então podemos usar o teorema do valor extremo

Passo 3

Começando achando a derivada da função:

d h d x = 2 d d t sec ⁡ 1 2 x

Aplicando a regra da cadeia e a derivada da secante:

d h d t = 2 1 2 sec ⁡ 1 2 x tan ⁡ 1 2 x  

d h d t = sec ⁡ 1 2 x tan ⁡ 1 2 x

Passo 4

Daí já dá pra ver que x = 0 é um valor extremo da função, que é aquele mínimo absoluto que dá pra ver no gráfico em 0 ,   2 . Agora precisamos do extremo absoluto que vemos no gráfico. Aquele extremo é o valor da função no limite superior. Vamos fazer f 1 2 π :

f 1 2 π = sec ⁡ 1 2 1 2 π tan ⁡ 1 2 1 2 π

f 1 2 π = sec ⁡ π 4 tan ⁡ π 4 = 2

Resposta

Mín. absoluto: f 0 = 2

Máx. absoluto: f 1 2 π = 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontrar a ,b ,c e d tal que a função f x = 2 a x 3 + b x 2 - c x + d tenha pontos críticos em x = 0 e x = 1 . Se a0 , qual deles é ponto de máximo, qual é ponto de mínimo?
Um fio de comprimento l é cortado em dois pedaços. Com um deles se fará um círculo e com o outro, um quadrado.Como devemos cortar o fio a fim de que a soma das duas áreas compreendidas pelas figuras s
1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .a) f é côncava para cima no intervalo I e tem exatamente um extremo relativo.
7-14. Localize todos os pontos críticos e identifique quais deles são pontos estacionários.9. f x = x + 1 x 2 + 3
2. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .c) f tem exatamente um ponto de inflexão e um extremo relativo em I .