Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 55
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos Exemplos 3 e 4 desta secção. Faça um esboço do gráfico da função no intervalo.
Passo 1
Como a função é condicional, ela provavelmente não segue a mesma regra das outras funções que só tem uma equação. Como ela muda de comportamento a partir de outra equação, vamos fazer o gráfico da função e ver como ele pode nos ajudar a determinar os máximos e mínimos absolutos da função.
Passo 2
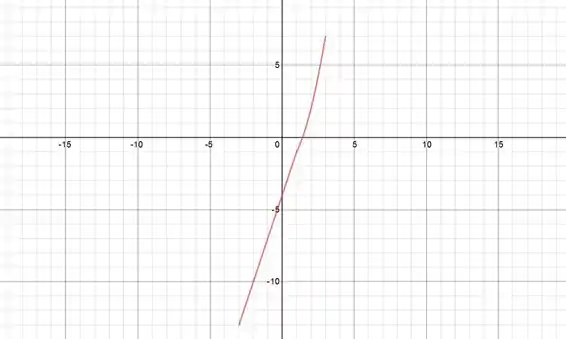
Vamos começar plotando a reta da primeira equação da função.
Essa reta passa pelos pontos e pelo ponto . É só ligar os dois pontos e teremos a reta:
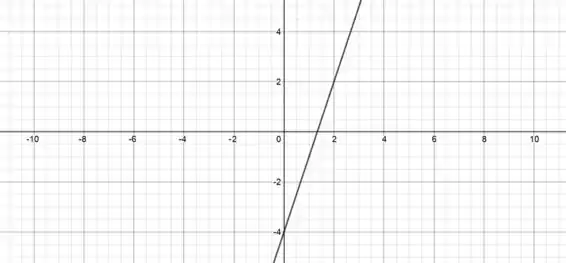
Mas a função só considera essa reta para . Ficamos então com:
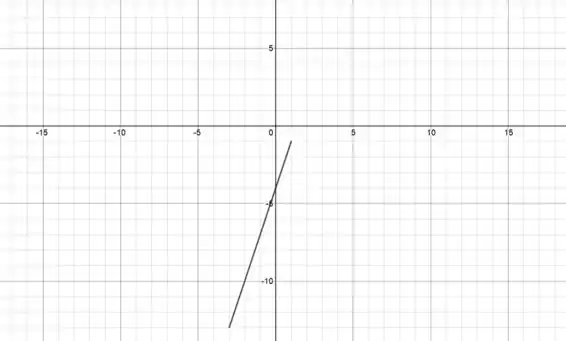
Passo 3
Na segunda equação da função, temos uma parábola deslocada em unidades em com concavidade para cima!
O gráfico fica:
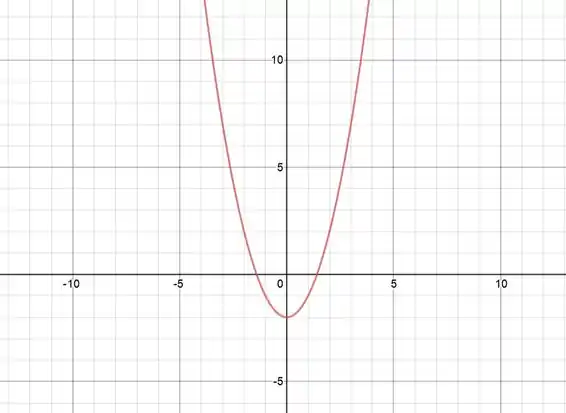
Mas só queremos a parábola para ! Então ficamos com o gráfico:
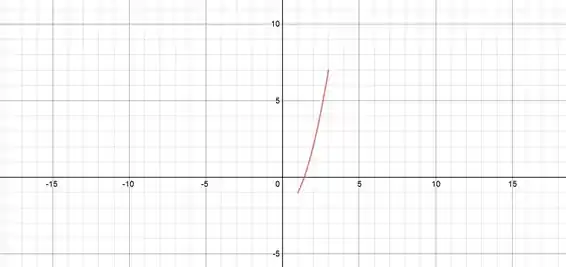
Passo 4
Juntando os dois gráficos, teremos o gráfico resultante da nossa :
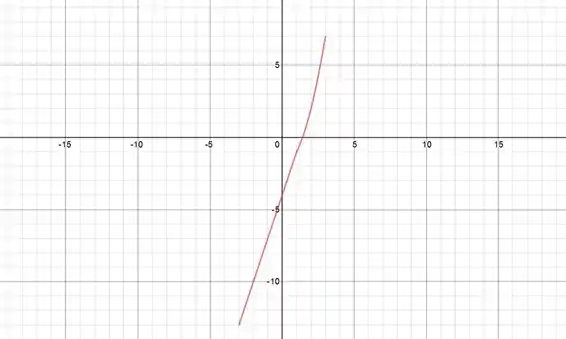
Passo 5
Vamos verificar se a função é contínua no ponto de interseção das duas curvas:
Para a reta:
Para a parábola:
Então a função é contínua!
Passo 6
Do gráfico, da pra ver que os pontos de máximo absoluto e de mínimo absoluto serão nos extremos do intervalo. O mínimo absoluto vai ser e o máximo absoluto vai ser em Calculando:
Mínimo:
Máximo:
Resposta
Mín. absoluto:
Máx. absoluto:
