Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 28
Ache o volume do sólido gerado pela rotação da região do Exercício 27 em torno da reta .
Passo 1
Bom no exercício 27, a região era limitada pela curva de vermelho na imagem abaixo e pela reta de roxo:
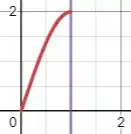
Então aplicaremos a equação do volume por invólucro cilíndrico:
Passo 2
A diferença aqui em relação ao exercício anterior é que a rotação não será mais em torno do eixo y, mas sim da reta . Com isso, precisamos substituir o x que está multiplicando a função f(x) por , os limites de integração serão por causa da curva e por causa da reta. Então podemos escrever a equação de volume da seguinte maneira:
Passo 3
Vamos resolver a integral para obtermos o volume, reescrevendo ela:
Integrando cada termo:
Substituindo os limites de integração:
Resposta
Exercícios de Livros Relacionados
40 – A região apresentada aqui gira em tomo do eixo y para gerar um sólido. Qual método ( do disco, do anel, da casca) você usaria para determinar o volume do sólido? Quantas integrais seriam necessár
39 – A região apresentada aqui gira em torno do eixo x para gerar um, sólido. Qual método (do disco, do anel, da casca) você usaria para determinar o volume do sólido? Quantas integrais seriam necessá
41 – Uma conta (de um colar) é feita de uma esfera de raio 5, ao se perfurar diametralmente a esfera usando uma broca de raio 3. A = Determine o volume da conta.
37 – A região no primeiro quadrante limitada em cima pela curva y = 1 x 1 4 a esquerda pela reta x = 1 16 e abaixo da reta y = 1 é girada em torno do eixo x para gerar um sólido. Determine o volume do
38 – A região no primeiro quadrante limitada em cima pela curva y = 1 x a esquerda pela reta x = 1 4 e abaixo da reta y = 1 é girada em torno do eixo y para gerar um sólido. Determine o volume do sóli