Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.2 - Ex. 41

Ache o volume do sólido gerado pela rotação da região do Exercício 39 em torno do eixo x.

Passo 1

Bom, o Exercício 39 nos deu a região limitada pela curva y = s e n 2 x e pelo eixo x de x = 0   a x = π . Vamos esboçar em um gráfico para facilitar a visualização da região:

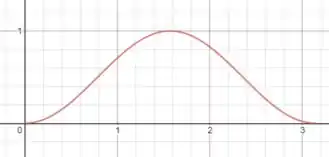
Como iremos rotacionar essa região em torno do eixo x, vamos utilizar a equação do volume pelo método dos discos:

V = π ∫ a b f x 2 d x

Passo 2

Substituindo os limites de integração e a função f x pela curva y, nossa integral passa a ser:

V = π ∫ 0 π s e n 4 x d x

Passo 3

Agora resolvendo a integral, podemos reescrevê-la como:

V = π ∫ 0 π s e n 2 x s e n 2 x d x

Pela relação trigonométrica:

s e n 2 x = 1 - c o s 2 x 2

Ficamos com:

V = π ∫ 0 π 1 - c o s 2 x 2 2 d x

Abrindo a potência:

V = π 4 ∫ 0 π 1 - 2 c o s 2 x + c o s 2 2 x d x

Usando outra identidade:

c o s 2 x = 1 + c o s 2 x 2

Ficamos com:

V = π 4 ∫ 0 π 1 - 2 c o s 2 x + 1 + c o s 4 x 2 d x

Integrando cada termo:

V = π 4 3 2 x - s e n 2 x + s e n 4 x 8 π 0

V = 3 π 2 8

Resposta

V = 3 π 2 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

36) Ache o volume do solido gerado pela rotação da região do exercício 35 em torno do eixo x.
Questão: 41A densidade linear de uma barra num ponto a x m de um extremo é 2 e - x kg/m. Se a barra tiver 6 m de comprimento, ache a massa e o centro de massa da barra.
Questão: 40 Ache o volume do solido gerado pela rotação em torno do eixo x da região do Exercício 39.
Considere a região delimitada pelos gráficos de y=t g - 1 x , y= 0 e x =1 . a. Determine a área da região. b. Determine o volume do sólido formado pela rotação dessa região em torno do eixo das ordena
Nos Exercícios 15-18, determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo dado.16- Em torno do eixo y