Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.2 - Ex. 43

Ache o volume do sólido gerado pela rotação da região do Exercício 39 em torno da reta .

Passo 1

Bom, o Exercício 39 nos deu a região limitada pela curva e pelo eixo x de a . Para termos uma noção melhor da região vamos usar a imagem:

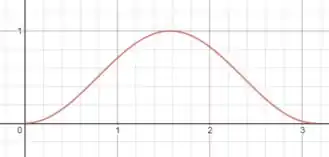
Como queremos rotacionar em torno de uma reta horizontal, podemos usar a equação de volume pelo método dos discos:

Passo 2

Nossa será escrita como a diferença entre o eixo onde iremos fazer a rotação e a curva que limita a região:

E os limites de integração serão e a equação do volume então ficará:

Passo 3

Agora precisamos resolver a integral, primeiro vamos resolver a potência:

Usando a identidade trigonométrica:

A integral fica:

Resolvendo a potência:

Fazendo a subtração e colocando em evidência:

Usando a identidade:

A integral se escreve:

Integrando termo a termo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

55- Determinação de volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados e pela curva y = cos ⁡ x ,0 ≤ x ≤ π / 2 , em tornoDo eixo

56- Determinação de volume Determine o volume do sólido gerado pela rotação da região delimitada pelo eixo das abcissas e pela curva y = x s e nx , 0 ≤ x ≤ π , em tornoDa reta x = π Veja o gráfico do

57- Considere a região delimitada pelos gráficos de y = ln ⁡ x , y = 0 e x = e .Determine a área da regiãoDetermine o volume do sólido formado pela rotação dessa região em torno do eixo das abscissas.

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : x 2 ≤ y ≤ x

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que : x 2 + ( y - 2 ) 2 ≤ 1