Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.1 - Ex. 57

57- Considere a região delimitada pelos gráficos de y = ln ⁡ x , y = 0 e x = e .

  1. Determine a área da região
  2. Determine o volume do sólido formado pela rotação dessa região em torno do eixo das abscissas.
  3. Determine o volume do sólido formado pela rotação dessa região em torno da reta x = - 2 .
  4. Determine o centroide da região

Passo 1

Fala galera! Vamos começar uma questão da maneira como ela deveria começar. Pelo começo! Vamos ver a letra a)

Antes de fazer o cálculo da área primeiramente temos que saber a região de limitação da nossa região né? Ele deu que y vai de 0 até ln ⁡ x , beleza mas e x ? Vai de quanto a quanto?

0 = ln ⁡ x → e 0 = x → 1

Então x vai de 1 até e , belezura.

O que nos dá uma área que pode ser calculada por:

A = ∫ 1 e ln ⁡ x   d x

Mas você sabe quanto vale a integral imprópria de ln ⁡ x ? Vamos resolver aqui rapidex.

u = ln ⁡ x → d u = 1 x

d v = d x → v = x

Substituindo em:

∫ u d v = u v - v d u

Temos:

∫ l n x   d x = x l n   x - ∫ x 1 x d x  

∫ l n   x d x = x l n   x - x

Agora vamos aplicar o intervalo de x indo de 1 até e :

A = x l n   x - x 1 e

A = [ e l n   e - e - ( 1 ln ⁡ 1 - 1 ) ]  

Como ln ⁡ e = 1 e ln ⁡ 1 = 0 , então:

A = e - e - 0 + 1 = 1   u A

Onde u A é unidade de área.

Passo 2

Agora vamos para a b) só que primeiro vamos plotar a região para que fique fácil visualizar as coisas!

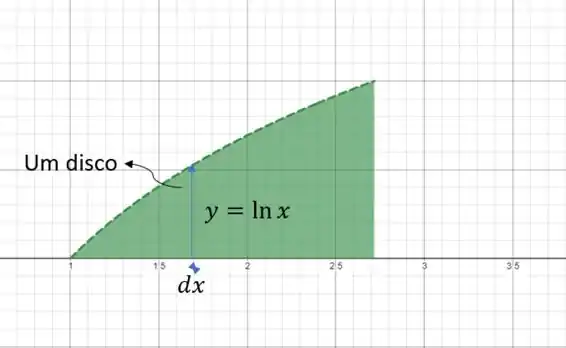
Rotação pelo eixo das abcissas é a rotação em relação do eixo x , logo o eixo y será o raio de cada disco de altura d x , considerando que vamos resolver pelo método dos discos.

V = π ∫ 1 e ln 2 ⁡ x   d x

Fazendo integração por partes nessa função temos:

u = ln 2 ⁡ x → d u = 2 ln ⁡ x x

d v = d x → v = x

Substituindo na equação de integração por partes temos:

∫ ln 2 ⁡ x   d x = x l n 2 x - 2 ∫ l n   x

∫ ln 2 ⁡ x = x l n 2 x - 2 x l n   x + 2 x

Aplicando o intervalo temos:

V = π [ e l n 2 e - 2 e l n   e + 2 e - 0 - 0 + 2 ]

V = π [ e - 2 e + 2 e - 2 ]

V = π e - 2 u V

Passo 3

Já para a letra c a rotação em x = - 2   nos dá a seguinte região de giro.

O que nos dá o seguinte volume, fazendo por cascas cilíndricas:

V = 2 π ∫ 1 e x + 2 ln ⁡ x d x

Onde x + 2 é o raio da casca cilíndrica (2 da distância da reta de giro com a origem e x a distância de um ponto qualquer dessa região com a origem), ln ⁡ x   a altura de cada casca cilíndrica e d x a espessura de casca cilindrica.

V = 2 π ∫ 1 e x l n   x   d x + ∫ 1 e 2 ln ⁡ x   d x

Fazendo a integração por partes de x   l n x :

u = x → d u = d x

d v = ln ⁡ x → v = x l n x - x

Logo:

∫ x l n x = x 2 ln ⁡ x - x 2 - ∫ x l n   x + ∫ x

2 ∫ x l n   x = x 2 ln ⁡ x - x 2 + x 2 2 = x 2 ln ⁡ x - x 2 2

Logo:

∫ x l n   x = x 2 ln ⁡ x 2 - x 2 4

Substituindo o resultado na integral do volume temos:

V = 2 π x 2 ln ⁡ x 2 - x 2 4 1 e + 2 π 2 ( x l n   x - x ) 1 e

V = 2 π e 2 ln ⁡ e 2 - e 2 4 - 1 × 0 2 - 1 4 + 4 π e l n   e - e - 1 ln ⁡ 1 + 1

V = 2 π e 2 2 - e 2 4 + 1 4 + 2 π 2

V = 2 π e 2 4 + 1 4 + 2

V = 2 π e 2 + 9 4 = π 2 e 2 + 9   u V

Passo 4

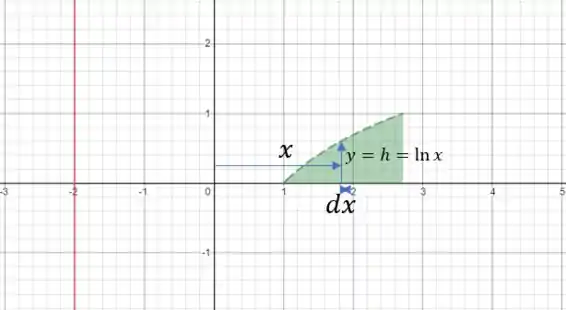
Para a letra d vamos traçar uma linha vertical qualquer na nossa região. Com um centro em x m ,   y m

Temos que o comprimento dessa linha L é o tamanho da própria função:

L = ln ⁡ x

Como sua largura é d x , logo seu elemento de área valerá:

d A = ( ln ⁡ x ) d x

Calculando á área no intervalo de x indo de 1 até e temos a resposta da letra a que é 1.

Sua coordenada x m será x pois essa linha está em uma coordenada qualquer de x e seu y m obrigatoriamente estará na metade do comprimento da linha e será:

y m = ln ⁡ x + 0 2

Calculando y - temos:

y - = ∫ y m d A ∫ d A

y - = 1 2 ∫ 1 e ln 2 ⁡ x   d x 1

E da letra b podemos dizer que essa integral vale:

∫ ln 2 ⁡ x = x l n 2 x - 2 x l n   x + 2 x

Logo, aplicando o intervalo:

y - = 1 2 e - 2 e + 2 e - 2 = e - 2 2

E calculando x - :

x - = ∫ x m d A ∫ d A

x - = ∫ 1 e x ln ⁡ x d x

E da letra c podemos dizer que essa integral vale:

∫ x l n   x = x 2 ln ⁡ x 2 - x 2 4

Logo, aplicando o intervalo:

x - = e 2 + 1 4

Resposta

  1. A = 1   u A
  2. V = π e - 2 u V
  3. V = π 2 e 2 + 9 u V
  4. x - , y - = e 2 + 1 4 , e - 2 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7 - Determine o volume do sólido gerado pela rotação da região limitada pelo eixo x, pela curva y = 3 x 4 e pelas retas x = 1 e x = - 1 em torno:B - do eixo y;O limite de integração para este método s
7 - Determine o volume do sólido gerado pela rotação da região limitada pelo eixo x, pela curva y = 3 x 4 e pelas retas x = 1 e x = - 1 em torno:B - do reta x = 1;
36) Ache o volume do solido gerado pela rotação da região do exercício 35 em torno do eixo x.
Questão: 41A densidade linear de uma barra num ponto a x m de um extremo é 2 e - x kg/m. Se a barra tiver 6 m de comprimento, ache a massa e o centro de massa da barra.
Questão: 40 Ache o volume do solido gerado pela rotação em torno do eixo x da região do Exercício 39.