Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1g
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :
Passo 1
Esse problema inicialmente terá que ter um mecanismo um pouco diferente, pois você já deve ter notado que normalmente é dado o intervalo de integração.
De alguma forma, vamos achar esse intervalo e você verá como faremos isso!
Faremos separadamente os gráficos de cada membro da desigualdade, ou seja:
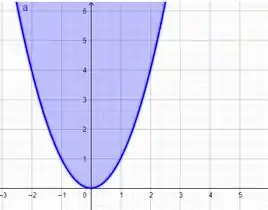
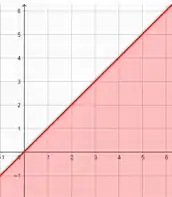
E agora a interseção entre esses dois gráficos, que estará representado de Verde!
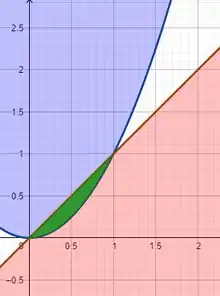
Passo 2
Agora vem a parte de analisar os gráficos para conseguirmos extrair informações importantes:
Lembra que temos que achar o intervalo de integração né?
Iremos fazer igualando as duas funções e as raízes dessa equação serão os intervalos:
Raízes , entãooo nosso primeiro problema já foi concluído, sabemos os intervalos e de forma bem tranquila!
Para calcularmos o volume, faremos o volume da curva menos o volume da curva , nos limites já explicados no parágrafo anterior, primeiro uma colher de chá, caso você não lembre a fórmula:
Passo 3
Agora focaremos em resolver essas integrais. Vamos lá que nisso, vocês são craques!!!
( ):
Finalmente, conseguiremos chegar aquilo em que tanto queríamos, não é a sua formatura, mas pode ficar feliz com essa conquista!!