Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 27
Ache o volume do sólido gerado pela rotação, em torno do eixo y, da região limitada pelo gráfico de pelo eixo x e pela reta .
Passo 1
A imagem abaixo mostra a região que iremos precisar integrar e aplicar a rotação:
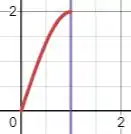
A linha vermelha mostra a parte da curva limitada pela linha roxa, que é a reta . Aplicaremos então a equação do volume por invólucro cilíndrico:
Passo 2
Como a rotação é em torno do eixo y, não precisaremos adaptar o que há dentro da integral para fazermos a rotação. Então basta substituir a curva y no lugar de f(x). Os limites de integração serão até a reta .
Ficaremos então com:
Passo 3
Resolvendo a integral:
Resposta
Exercícios de Livros Relacionados
Resolva o Exercício 16, se os dois planos estiverem em lados diferentes opostos em relação ao centro da esfera, mas todos os demais permanecem os mesmos.
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados
Ache o volume do sólido gerado pela rotação da região limitada pela curva de y = | x - 2 | , pelo eixo x , e pelas retas x = 1 e x = 4 , em torno do eixo x .
Use integração para encontrar o volume de sum segmento de uma esfera, se ela tiver um raio de r unidades e se a altura do segmento for h unidades.
A base do sólido é a região encerrada por um círculo tendo um raio de r unidades, e toda a secção plana perpendicular a um diâmetro fixo da base é um quadrado cuja diagonal é uma corda do círculo. Ach