Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 38
38. A região do primeiro quadrante, limitada pela curva pelo eixo y e pela reta faz uma rotação em torno do eixo x. Ache o volume do sólido gerado.
Passo 1
Antes de tudo, vamos esboçar esse sólido de revolução,
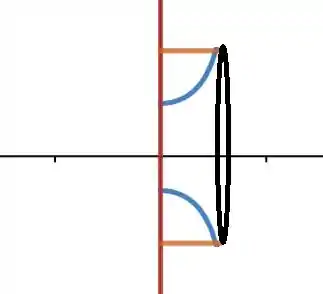
Em azul é referente a curva em marrom é a curva y=2, e em vermelho é o eixo y.
Agora vamos cortar um pedaço desse sólido,
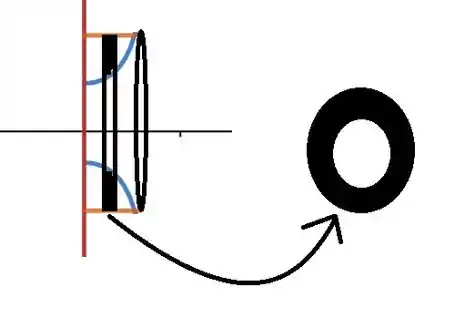
A direita na imagem está um anel que obtemos ao fatiar o sólido.
Passo 2
A área do anel que desejamos é dado pela área com o raio maior menos a área do raio menor, ou seja,
Passo 3
Lembrando que o volume é dado pela seguinte integral:
Portanto, a integral ficará assim:
Sabe de onde vem esse é ponto de intersecção das duas curvas, então, basta fazer secx=2
Então, realmente o x está variando entre 0 à .
Continuando,
Resposta
Exercícios de Livros Relacionados
Determinar o volume do sólido de revolução gerado pela rotação das regiões indicadas, ao redor dos eixos dados. x = y 2 e x = 2 - y 2 ; ao redor do eixo dos y
Determinar o volume do sólido gerado pela rotação, em torno da reta y = 2 , da região limitada por y = s e nx ,y = s e n 3 x ,x = 0 ,ex = π 2 .
Determinar o volume do sólido gerado pela rotação, em torno da reta y = - 2 , da região limitada por y = cos x ,y = - 2 ,x = 0 ,ex = 2 π .
7. y = x 2,y = x 3
6. y = ln x,y = - 1 ,y = 2ex = 0