Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 12
Use integração para encontrar o volume de sum segmento de uma esfera, se ela tiver um raio de unidades e se a altura do segmento for unidades.
Passo 1
Pessoal, para resolver essa questão nós vamos utilizar o método dos cortes e para utilizá-lo precisamos achar a fórmula da área de uma secção perpendicular genérica.
Abaixo eu tenho a figura da esfera de raio e uma secção perpendicular (em vermelho).
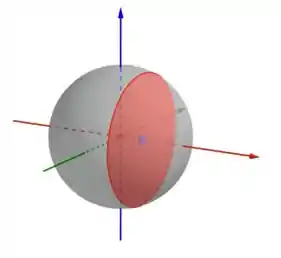
Perceba que um segmento esférico de altura seria obtido se a gente cortasse um pedaço da esfera no intervalo , esse intervalo tem justamente o comprimento . Então, para achar o volume do segmento esférico, podemos achar a área da secção transversal e usar a fórmula dos cortes.
Vamos considerar o eixo azul (OY) e o eixo vermelho (OX), a secção transversal é a área do círculo, sendo o raio dado por , isso vem da fórmula . Dessa forma, a área da secção será dada por:
Passo 2
Agora, vamos lembrar a fórmula que calcula o volume. Seja um sólido tal que esteja entre planos perpendiculares ao eixo em e . Se a medida da área da secção plana de no plano perpendicular ao eixo em for dada por , onde é contínua em , então a medida do volume de será dada por:
No nosso exemplo, e o intervalo de integração é . Dessa forma,
Passo 3
Já podemos resolver a integral. Sabemos da integral definida que:
Em que é uma primitiva de .
Dessa forma,
Sendo assim, o volume é.