Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 30
Ache o volume do sólido gerado pela rotação, em torno do eixo y, da região limitada pelo gráfico de , pelo eixo x e pela reta .
Passo 1
Vamos colocar a região delimitada em uma figura para facilitar a visualização:
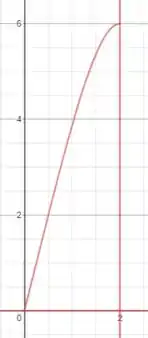
Usaremos a equação de volume por invólucro cilíndrico para fazermos a rotação em torno do eixo y:
Passo 2
Como a rotação é em torno do eixo y, não precisamos alterar o integrando, e a f(x) será a própria curva dada no enunciado:
Os limites serão dados por delimitado pela curva e delimitado pela reta na direita. Nossa integral vai ficar:
Passo 3
Vamos agora resolvê-la, reescrevendo a integral acima:
Integrando cada termo:
Substituindo os limites:
Resposta
Exercícios de Livros Relacionados
Ache o volume do sólido gerado pela rotação em torno da reta y = - 1 da região acima do eixo x limitada pela reta 2 y = x + 3 e pelas curvas y 2 + x = 0 , y 2 - 4 x = 0 de x = - 1 a x = 1 .
Use o método das cascas cilíndricas para encontrar o volume pela rotação da região delimitada pelas curvas em relação ao eixo dado y = x 2 ,y = 6 x - 2 x 2
Use o método das cascas cilíndricas para encontrar o volume pela rotação da região delimitada pelas curvas em torno do eixo x x y = 1
Use o método das cascas cilíndricas para encontrar o volume pela rotação da região delimitada pelas curvas em relação ao eixo dado y = x 4 ,y = 0 ,x = 2 eixo y
Considere s o solido obtido pela rotação da região mostrada na figura em torno no do eixo y . Explique por que é complicado usar fatias para encontrar o volume V de S. Esboce uma casca de aproximação