Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 13
Ache o volume do sólido gerado pela rotação em torno da reta da região acima do eixo limitada pela reta e pelas curvas , de a .
Passo 1
Se plotarmos essas funções em um gráfico para ajudar a nossa visualização, teremos o seguinte:
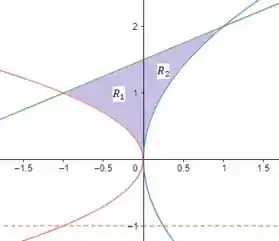
No qual:
A função em verde é ;
A função em vermelho é ;
A função em azul é ;
A linha pontilhada em laranja é o eixo de rotação .
Passo 2
Se observamos o gráfico, notaremos que há uma região chamada de que está à esquerda da origem e outra região, chamada de , que está à direita da origem. Quando isso ocorre, o que temos que fazer é calcular o volume de cada região separadamente e depois somar seus resultados, ok? Seja o volume total das regiões, teremos:
Como o eixo de rotação não toca a região em questão, um método interessante de utilizarmos é o método do anel. Esse método nos diz o seguinte:
No qual e são, respectivamente, o raio externo e interno do sólido.
Passo 3
Agora que já sabemos o que temos que fazer, vamos utilizar esse raciocínio para calcular . Para a primeira região, o raio externo é a função em verde e o raio interno é a função em vermelho, não é mesmo? Sendo assim, teremos:
Utilizando a integral supracitada no passo 2, teremos:
Resolvendo a integral, teremos:
Passo 4
Uma vez calculado , vamos utilizar o mesmo raciocínio do passo anterior para calcular ! Para a segunda região, o raio externo é a função em verde e o raio interno é a função em azul, certo? Sendo assim, teremos:
Utilizando a integral supracitada no passo 2, teremos:
Resolvendo a integral, teremos:
Passo 5
Agora que já encontramos e , temos que o volume total do sólido será: