Ache o volume do sólido gerado pela rotação da região limitada por aquela reta e pela parábola x 2 = 4 y em torno da reta y = 1 . Tome os elementos retangulares de área paralelos ao eixo de revolução.

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 35

Ache o volume do sólido gerado pela rotação da região limitada por aquela reta e pela parábola em torno da reta . Tome os elementos retangulares de área paralelos ao eixo de revolução.

Passo 1

Vamos utilizar a imagem abaixo para facilitar a visualização da região limitada:

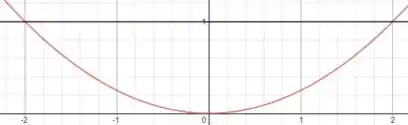
A reta horizontal preta é o eixo que iremos usar como rotação. Usaremos a equação do volume por invólucro cilíndrico:

Passo 2

Como o enunciado nos pede para tomar elementos retangulares de área horizontais, nossa integral será escrita em termos de y. como o eixo está deslocado em relação à origem, substituiremos o x na equação por . E usaremos apenas o lado direito da região no desenho, porque ela é simétrica em relação ao eixo y.Nossa integral então ficará:

Os limites de integração serão os valores de y onde a curva limita, e onde a reta preta limita, , ficaremos com:

Passo 3

Agora vamos resolver a integral, primeiro vamos reescrever o integrando:

Integrando cada termo:

Substituindo os limites de integração:

E então multiplicaremos por 2 para obtermos o volume de toda a região:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método das cascas cilíndricas para achar o volume gerado pela rotação ao redor do eixo x da região limitada pelas curvas dadas. Esboce a região e a casca típica. y = 4 x 2 , 2 x + y = 6

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região limitada pelas curvas dadas ao redor dos eixos especificados. Esboce a região e a casca típica. y = x 2 , y = 0 ,

A região limitada pelas curvas dadas é girada ao redor dos eixos especificados. Ache o volume do solido resultante por qualquer método y = x 2 + x - 2 , y = 0 ; ao redor do eixo x

Use a Regra do Ponto Médio com n = 4 para estimar o volume obtido pela rotação ao redor do eixo y da região sob a curva y = t g x , 0 ≤ x ≤ π / 4

A região limitada pelas curvas dadas é girada ao redor dos eixos especificados. Ache o volume do solido resultante por qualquer método. x 2 + y - 1 2 = 1 ; ao redor do eixo x