Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.3 - Ex. 9
Use o método das cascas cilíndricas para encontrar o volume pela rotação da região delimitada pelas curvas em torno do eixo :
Passo 1
Opa, bora resolver essa questão! O enunciado pede pra a gente encontrar o volume do sólido obtido pela rotação da região delimitada pelas seguintes curvas:
E:
Colocando isso em um gráfico temos:
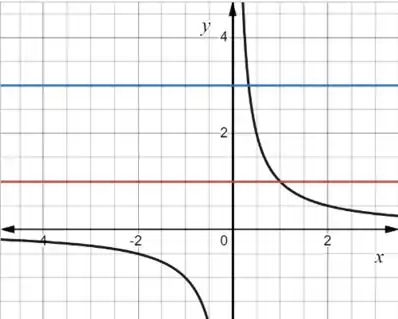
Ou seja, essa região azulzinha vai ser rotacionada em torno do eixo . O volume do sólido que a gente obtem é dada por:
Vamos colocar a mão na massa!
Passo 2
Os intervalos de interação vão ser dados por:
Pela formula de volume em torno do eixo :
Integrando:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo y da região limitada pelas curvas dadas. Esboce a região e uma casca típica. y = x 2 ,y = 0 ,x = 1
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica. y = x 2 ,y = 2 -
Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. y = x 3 ,y = 8
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado.
Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. x = 4 y 2 - y