Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 42

Ache o volume do sólido gerado pela rotação em torno do eixo y, da região limitada pelo gráfico de e pelas retas , , e . Tome os elementos de área retangulares paralelos ao eixo de revolução.

Passo 1

Vamos primeiro fazer um esboço da região que é tratada no enunciado:

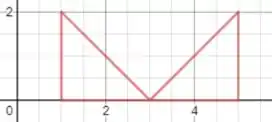
Como se trata da rotação em torno do eixo y, vamos usar a equação de volume por invólucro cilíndrico:

Passo 2

Vamos separar a nossa região na soma de duas funções, o triangulo da esquerda e o triangulo da direita. Como a questão pede elementos de retangulares paralelos ao eixo de revolução, serão elementos verticais, e portanto, estaremos integrando em x.

O triângulo da esquerda será escrito como:

E o da direita:

Nossa integral de volume então será separada em duas:

Os primeiro dois limites de integração serão da reta até o ponto onde a função é descontínua . E os dois últimos é da descontinuidade até a reta .

Nossas integrais ficam então:

Passo 3

Resolveremos primeiro as integrais indefinidas:

A primeira ficará:

Integrando:

Substituindo os limites:

Para o volume do outro triângulo, a segunda integral fica:

Integrando cada termo:

Substituindo os limites de integração:

Somando os dois volumes:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo y da região limitada pelas curvas dadas. Esboce a região e uma casca típica. y = x 2 ,y = 0 ,x = 1

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica. y = x 2 ,y = 2 -

Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. y = x 3 ,y = 8

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado.

Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. x = 4 y 2 - y