Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.3 - Ex. 18
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica.
em torno de
Passo 1
Opa! Bora pra mais uma?!
O enunciado nos pede pra usarmos o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas:
em torno de
A formula para o volume do sólido de rotação em relação ao eixo tem essa carinha aqui:
Onde:
Podemos então esboçar a região e uma casca típica:
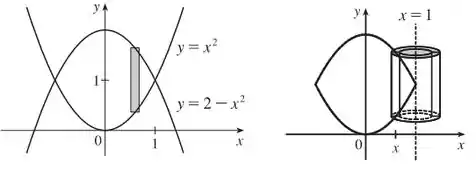
Passo 2
O círculo tem , e a circunferência tem perímetro , e altura . Com isso, temos o seguinte volume:
Usando o Teorema 5.5.7:
Resposta
Exercícios de Livros Relacionados
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x + y = 4 , x = y 2 - 4 y + 4
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . y = 4 - 2 x , y = 0 , x = 0 ; s o b r ex = - 1
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x = 2 y 2 , y ≥ 0 , x = 2 , s o b r ex = 2
Use o método de cascas cilíndricas para induzir o volume gerado girando a região delimitada pelas curvas dadas sobre o eixo especificado. y = x 3 , y = 8 , x = 0 ; s o b r ex = 3
Use o método de cascas cilíndricas para encontrar o volume gerado girando a região delimitada pelas curvas dadas em torno do eixo x . x = 2 y 2 , x = y 2 + 1 , s o b r ey = - 2