Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.3 - Ex. 10

Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo . Esboce a região e uma casca típica.

Passo 1

Eaee, belezinha?? Bom... queremos encontrar o volume do sólido obtido pela rotação da região delimitada pela seguinte curva dada:

Em torno do eixo .

Para isso, devemos utilizar o método das cascas cilíndricas. Mas que método é esse???

Esse método diz que o volume de um sólido obtido pela rotação em torno do eixo sob a curva de até é:

Agora vamos aplicar!! 😉

Passo 2

Podemos ver que a função varia de a em da seguinte forma:

Assim, o nosso intervalo de integração será .

Nesse sentido, aplicando o método das cascas cilíndricas, temos:

Passo 3

Assim, esboçando a região e a casca típica obtida pela rotação, temos:

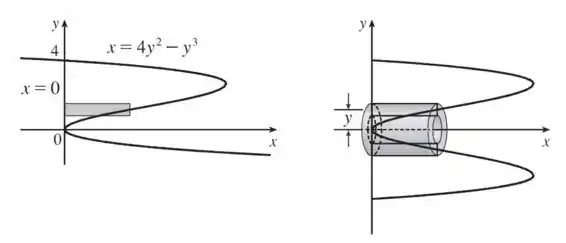
Entendeu direitinho?? Responde aee 😉

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo y da região limitada pelas curvas dadas. Esboce a região e uma casca típica. y = x 2 ,y = 0 ,x = 1

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica. y = x 2 ,y = 2 -

Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo x . Esboce a região e uma casca típica. y = x 3 ,y = 8

Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado.