Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo da região limitada pelas curvas dadas. Esboce a região e uma casca típica.
Passo 1
Esboço da região e de uma casca típica:
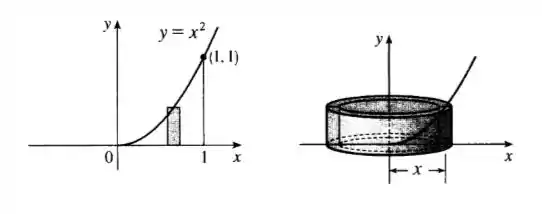
Passo 2
Calculo do volume:
Resposta
.