Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo . Esboce a região e uma casca típica.

Para calcular usando o método das cascas cilíndricas temos que usar a seguinte fórmula:

Onde corresponde a circunferência, a altura da casca e a espessura. Analisando a integral, precisamos achar quem é e quem são os limites de integração, vamos primeiro esboçar a região e uma casca para conseguir o que falta:

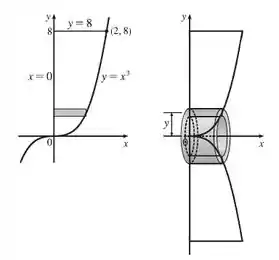
Nesta questão, nós temos que o cilindro estará deitado. Então a altura dele está indo do até a nossa função . Deste modo, temos que nossa altura é , pois vamos integrar em função de . Já os limites de integração são e .